Rudolf Taschner - Die Zahl, die aus der Kälte kam - Wenn Mathematik zum Abenteuer wird

Was für den Bauern mit seinen Feldern galt, das galt noch viel mehr für die Herrscher und Könige, die wissen wollten, über wie viel Land sie geboten. Bei ihren Feldzügen begleiteten sie die Geometer, die nach den gewonnenen Schlachten eifrig die Größe des eroberten Gebiets vermaßen.

Mit 6,2 Millionen Quadratkilometern war das von Alexander dem Großen in nur wenigen Jahren eroberte Weltreich gigantisch groß. Es erstreckte sich von Makedonien bis nach Indien, vom Kaspischen Meer bis zum Oberlauf des Nils. Erst das Imperium Romanum, das römische Weltreich, das unter Kaiser Trajan mit 8,3 Millionen Quadratkilometern seine größte Ausdehnung erfuhr, sollte es in der Antike noch übertreffen. Die Europäische Union ist im Vergleich dazu, obwohl sie von Skandinavien bis zum Mittelmeer, vom Atlantik bis zum Schwarzen Meer reicht, kleiner, nicht einmal 5 Millionen Quadratkilometer groß. Gleichgültig, ob sie über gewaltige oder über nicht so riesige Reiche verfügten, die einstigen Herrscher hätten gerne erfahren, wie viel von der ganzen Welt ihnen unterworfen war.

Eine Generation nach Alexander dem Großen gelang es Eratosthenes, dem Direktor der Bibliothek von Alexandria, die Größe der Erde zu messen: Am Mittag des 21. Juni jeden Jahres, wenn die Sonne am höchsten steht, warf der senkrecht errichtete Obelisk von Alexandria den kürzestmöglichen Schatten. Seine Länge ließ Eratosthenes genau vermessen und stellte aufgrund der ermittelten Daten fest, dass die Sonnenstrahlen zur lotrechten Richtung des Obelisken einen Winkel von 7 Grad und 12 Minuten, modern gesprochen: von 7,2 Grad aufspannten. Eratosthenes war weiterhin aufgefallen, dass die Sonne 800 Kilometer südlich von Alexandria, in der Stadt Syene am Oberlauf des Nils, an diesem Tag genau im Zenit stand. Ihre Strahlen trafen senkrecht auf die Erde; sie spiegelten sich damals im Wasser des tiefen Brunnens von Syene. Der Schatten des Obelisken, so schloss Eratosthenes, kam durch die Krümmung der Erde zustande. Denn dass die Erde Kugelgestalt besitzt, war spätestens seit Aristoteles allen gebildeten Griechen bewusst. Der Bogen des Großkreises auf der Erdkugel durch Syene und Alexandria, der dem Winkel von 7,2 Grad entspricht, ist 800 Kilometer lang. Den ganzen, den vollen Winkel von 360 Grad umfassenden Großkreis erhält man, wenn man die 7,2 Grad mit 50 multipliziert. So errechnete Eratosthenes, wie lang der Umfang dieses Großkreises ist: 800 Kilometer mit 50 multipliziert, 40 000 Kilometer.

So einfach diese Rechnung scheint, mit so vielen Unwägbarkeiten ist sie behaftet:

Woher, so stellt sich die erste Frage, wusste Eratosthenes, dass die Sonnenstrahlen in Syene und in Alexandria zueinander parallel stehen? Exakt parallel sind sie nicht, denn die Sonne ist nicht unendlich weit von der Erde entfernt. Doch schon zur Zeit des Eratosthenes waren sich die Gelehrten sicher: Der Abstand der Sonne zur Erde ist so riesengroß, dass man getrost von parallelen Sonnenstrahlen ausgehen darf.

Doch ist Syene, so stellt sich die nächste Frage, wirklich genau im Süden von Alexandria gelegen? Die Antwort lautet: nein. Syene befindet sich ein paar Grad östlich von Alexandria. Dadurch hat Eratosthenes in Wahrheit einen etwas größeren Wert als 40 000 Kilometer ermittelt, aber der Fehler liegt nur im einstelligen Prozentbereich.

Wieso konnte, so die dritte Frage, Eratosthenes den Umfang des Großkreises in Kilometern benennen? Konnte er natürlich nicht. Die Längeneinheit Kilometer war ihm unbekannt. Er benutzte die Einheit des Stadions. Und um der Wahrheit die Ehre zu geben: Ganz genau kennt man die Umrechnung des antiken Stadions, der von Eratosthenes verwendeten Längeneinheit, zum modernen Kilometer nicht. Aber wir wissen, dass Eratosthenes die Entfernung von Alexandria zu Syene mit dem Faktor 50 multiplizierte. Das ist der wesentliche Kern seiner Rechnung.

Schließlich kann man auf der modernen Landkarte schnell feststellen, dass sich Syene, jener antike Ort, wo sich heute Assuan befindet, nicht präzise auf dem nördlichen Wendekreis befindet. Ganz genau im Zenit steht die Sonne dort am 21. Juni zu Mittag nicht. Aber auch hier ist der Fehler so geringfügig, dass er das von Eratosthenes ermittelte Ergebnis nicht ernsthaft gefährdet.

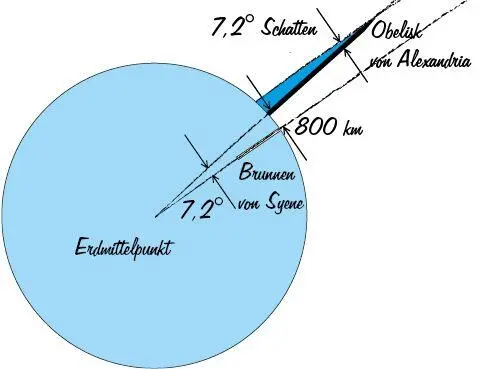
Abb. 2: Prinzip der Erdvermessung des Eratosthenes: Am 21. Juni jeden Jahres leuchtet zu Mittag der Sonnenstrahl in den Brunnen von Syene. Würde man ihn ins Erdinnere verlängern, landete er schließlich beim Erdmittelpunkt. Der zu ihm parallele Sonnenstrahl steht im nördlich gelegenen Alexandria nicht im Zenit: Der senkrechte Obelisk wirft einen Schatten von 7,2 Grad. Diese 7,2 Grad entsprechen dem Kreisbogen von Syene nach Alexandria, der 800 km lang ist. Dies ist genau ein Fünfzigstel des Erdkreises.

Wenn man von der Erdkugel weiß, wie lang der Umfang des Äquators ist, kann man mit Formeln, die Archimedes entdeckt hat, die Oberfläche der Erde ermitteln. Diese Formeln kannte man zu dieser Zeit bereits. Archimedes war nicht nur Zeitgenosse, sondern auch Bekannter des Eratosthenes. Das Ergebnis lautet: Die Erdoberfläche umfasst ungefähr 510 Millionen Quadratkilometer. Nicht einmal ein Prozent davon überdeckt die heutige Europäische Union. Aber auch das Reich Alexanders des Großen und das Imperium Romanum waren jeweils keine zwei Prozent der gesamten Erdoberfläche groß!

Kein Wunder, dass dieses Ergebnis die Herrscher und Könige erstaunte und dass nach Eratosthenes andere Geometer versuchten, die Größe der Erde erneut zu vermessen. Schon damals trat ein eigentümlicher Effekt zutage, den wir aus der Gegenwart nur zu gut kennen: Wenn es politisch opportun ist, bemühen sich Anpasser und Liebediener unter den Experten, den Herrschenden nach dem Mund zu reden. Wie von Geisterhand wurde die Erde plötzlich kleiner. Bis sie zur Zeit des Kaisers Trajan am Äquator nur mehr den Umfang von 27 000 Kilometer besaß – so jedenfalls behaupteten es die damals maßgebenden Geometer. Dadurch verkleinerte sich auch die Oberfläche der Erde beträchtlich: von den 510 Millionen Quadratkilometern des Eratosthenes zu weniger als halb so vielen 230 Millionen Quadratkilometern. Die Weltreiche begannen, sich ihren Namen zu verdienen.

Noch Christoph Kolumbus dürfte von der Annahme ausgegangen sein, die Erde habe am Äquator nur den Umfang von 27 000 Kilometern. Die Landmasse Europas und Asiens würde dann einen Großteil der Nordhalbkugel überdecken; die Entfernung von Lissabon bis zum chinesischen Quanzhou, von dem schon Ende des 13. Jahrhunderts der Venezianer Marco Polo berichtete, beträgt mehr als 11 000 Kilometer. Unter dieser Annahme konnte es Kolumbus wagen, auf der Westroute über den Atlantik China oder Indien erreichen zu wollen. Die Berater des portugiesischen Königshauses rieten davon ab, das Unternehmen zu finanzieren; sie vertrauten der alten Rechnung des Eratosthenes. Vom spanischen Hof wurde Kolumbus nach zähen Verhandlungen hingegen unterstützt, so dass er am 3. August 1492 in See stechen konnte. Bis zu seinem Lebensende war Kolumbus davon überzeugt, dass das Land, an dem er am 12. Oktober 1492 anlegte, „Hinterindien“ sei.

Eine falsche Messung ermöglichte die Entdeckung Amerikas.

Ist ein Kreis mit 40 000 Kilometer Umfang schon schwer vorstellbar,4 versagt unsere Vorstellungskraft völlig, wenn wir die Erde verlassen und kosmische Dimensionen in den Blick nehmen. Gar nicht lange nach Eratosthenes hatte der Astronom Hipparch den Abstand der Erde vom Mond vermessen. Sehr grob lässt sich dieser aufgrund der folgenden Beobachtung schätzen: Bei einer Mondfinsternis bedeckt der Erdschatten die Scheibe des Vollmonds. Der Rand des Erdschattens ist dabei immer kreisförmig – dies war, nebenbei erwähnt, für Aristoteles der Grund dafür, dass die Erde eine Kugel sein muss, denn nur ein kugelförmiger Körper wirft in jeder seiner Positionen einen kreisrunden Schatten. Hält man bei einer Mondfinsternis eine Ein-Euro-Münze eine Armlänge, also etwa 75 Zentimeter vom Auge entfernt in Richtung Mond, stimmt der Rand der Münze ziemlich genau mit dem Schattenrand der Erde überein. Weil der Rand der Münze etwa 75 Millimeter Umfang hat und die Münze zehnmal weiter vom Auge entfernt gehalten wurde, als ihr Umfang beträgt, kann man daraus schließen, dass der Mond rund zehnmal weiter von der Erde entfernt ist, als der Erdumfang beträgt. Das ergibt einen geschätzten Mondabstand von 400 000 Kilometern. Im Vergleich zum genau vermessenen mittleren Abstand des Mondes von der Erde von 384 000 Kilometern ist das keine üble Schätzung. Hipparch selbst hatte eine weitaus ausgeklügeltere Methode ersonnen,5 mit der er den Abstand zwischen Erde und Mond bis auf wenige Prozent genau bestimmen konnte.