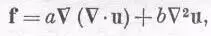
что как раз дает (39.32) с другим определением постоянных. Вас может удивить, почему у нас нет третьего слагаемого СXСXu, которое тоже вектор. Но вспомните, что СXСXu
в точности равно С 2u-С(С·u), т. е. это линейная комбинация двух уже написанных слагаемых. Так что оно не добавит ничего нового. Мы еще раз доказали, что в изотропном материале есть только две упругие постоянные.
Для получения уравнения движения материала мы можем положить выражение (39.32) равным r д 2 u /дt 2 и, пренебрегая объемными силами типа силы тяжести, написать
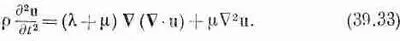
Это уравнение выглядит похожим на волновое уравнение, с которым мы познакомились в электромагнетизме, за исключением одного добавленного слагаемого, которое усложняет дело. Для материалов, упругие свойства которых всюду одинаковы, мы можем увидеть, на что похоже общее решение. Вы, наверное, помните, что любое векторное поле может быть записано в виде суммы двух векторов, у одного из которых нулю равна дивергенция, а у другого — ротор. Другими словами, можно положить

где
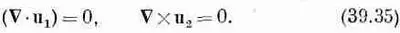
Подставляя вместо uв уравнении (39.33) u 1+ u 2, получаем
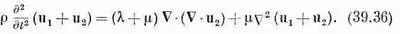
Взяв дивергенцию этого уравнения, мы можем исключить из него u 1:
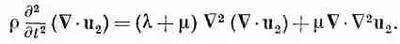
Поскольку операторы С 2и С могут быть переставлены, можно вынести оператор дивергенции и получить
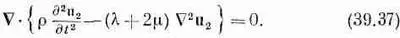
А так как СX u 2, по определению, равно нулю, то ротор выражения в фигурных скобках также будет нулем, так что выражение в скобках само по себе тождественно равно нулю и
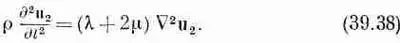
Это векторное волновое уравнение для волн, движущихся со скоростью С 2= Ц(l+2m)/r. Поскольку ротор u 2есть нуль, то эти волны не связаны со сдвигом, а представляют просто волны сжатия наподобие звуковых, которые мы изучали в предыдущих главах и скорость которых как раз равна найденной нами для С прод.
Подобным же образом, беря ротор уравнения (39.36), можно показать, что u 1удовлетворяет уравнению

Это снова векторное волновое уравнение для волн, распространяющихся со скоростью C 2 =Цm/r. Поскольку С· u 1равно нулю, то перемещение u 1 не приводит к изменению плотности; вектор u 1соответствует поперечным или сдвиговым волнам, которые встречались нам в предыдущей главе, а
C 2=C сдвиг.
Если мы хотим знать статические напряжения в изотропном материале, то в принципе их можно найти, решая уравнение (39.32) с f, равным нулю (или равным статическим объемным силам, обусловленным силой тяжести, такой, как rg) при определенных условиях, связанных с силами, действующими на поверхности нашего большого куска материала. Сделать это несколько сложнее, чем в соответствующих задачах электромагнетизма. Во-первых, это более трудно потому, что сами уравнения несколько сложнее, и, во-вторых, формы тех упругих тел, которыми мы обычно интересуемся, гораздо сложнее. На лекциях по электричеству мы часто интересовались решением уравнений Максвелла в областях сравнительно простой геометрической формы, таких, как цилиндр, сфера и т. д. В теории упругости, нам приходится заниматься объектами гораздо более сложной формы, например крюком подъемного крана, или коленчатым автомобильным валом, или ротором газовой турбины. Такие задачи иногда можно приближенно решить численным методом, воспользовавшись принципом минимальной энергии, о котором мы упомянули ранее. Другой способ — это воспользоваться моделями предметов и измерять внутренние напряжения экспериментально с помощью поляризованного света.
Читать дальше

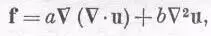
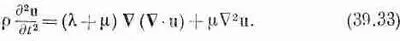

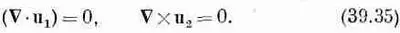
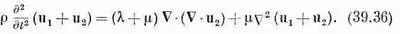
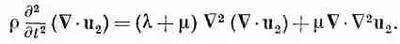
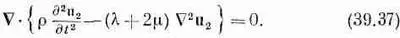
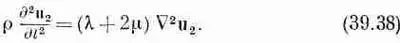




![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
