где
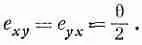
Теперь вы сочтете, что при неоднородной деформации обобщенную деформацию сдвига можно описать, определив величины е xy и е yx следующим образом:
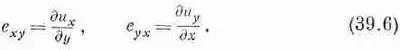
Однако здесь есть некая трудность. Предположим, что перемещения u х и u y имеют вид
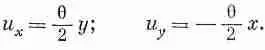
Они напоминают уравнения (39.4) и (39.5), за исключением того, что при u y стоит обратный знак. При таком перемещении маленький кубик из желе претерпевает простой поворот на угол q/2 (фиг. 39.4).
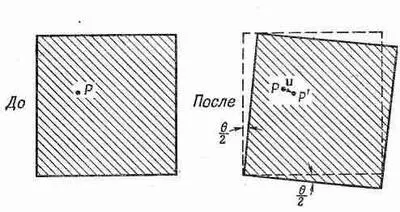
Фиг. 39.4. Однородный поворот. Никаких деформаций нет.
Никакой деформации здесь вообще нет, а есть просто вращение в пространстве. При этом никакого возмущения материала не происходит, а относительное положение всех атомов совершенно не изменяется. Нужно как-то устроить так, чтобы чистое вращение не входило в наше определение деформации сдвига. Указанием может послужить то, что если дu y /дх и дu x /ду равны и противоположны, никакого напряжения нет; этого можно добиться, определив
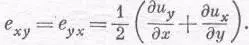
Для чистого вращения оба они равны нулю, но для чистого сдвига мы получаем, как и хотели, е ху =е у x .
В наиболее общем случае возмущения, который наряду со сдвигом может включать растяжение или сжатие, мы будем определять состояние деформации заданием девяти чисел:
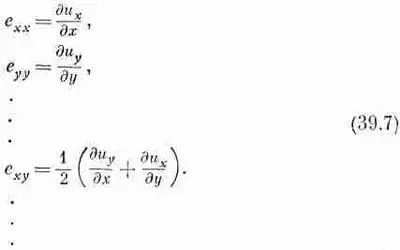
Они образуют компоненты тензора деформации. Поскольку тензор этот симметричен (согласно нашему определению, е ху всегда равно е ух ) , то на самом деле различных чисел здесь только шесть. Вы помните (см. гл. 31) общее свойство всех тензоров — элементы его преобразуются при повороте подобно произведению компонент двух векторов. (Если А и В — векторы, то С ij =А i В j — тензор.) А каждое наше e ij есть произведение (или сумма таких произведений) компонент вектора
u= (u х , u у , u z ) и оператора С=( д / д x, д / д y, д / д z), который, как
мы знаем, преобразуется подобно вектору. Давайте вместо х, у и z писать x 1 , x 2 и x 3, а вместо u х , u y и u г писать u 1, u 2и u 3 ; тогда общий вид элемента тензора e ij будет выглядеть так:

где индексы i и j могут принимать значения 1, 2 или 3.
Когда мы имеем дело с однородной деформацией, которая может включать как растяжения, так и сдвиги, то все e ij — постоянные, и мы можем написать
u х =е хх х+е ху y+е х z г. (39.9)
(Начало координат выбрано в точке, где и равно нулю.) В этих случаях тензор деформации e ij дает соотношение между двумя векторами — вектором координаты r=(x, y, z) и вектором перемещения u= (u х , u у , u г ).
Если же деформация неоднородна, то любой кусочек желе может быть как-то искажен и, кроме того, могут возникнуть местные повороты. Когда все возмущения малы, мы получаем
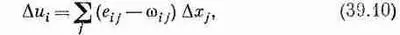
где w ij, — антисимметричный тензор
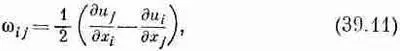
описывающий поворот. Нам незачем беспокоиться о поворотах; займемся только деформацией, которая описывается симметричным тензором е ij .
Читать дальше

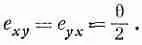
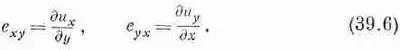
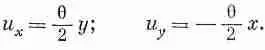

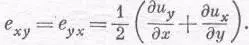
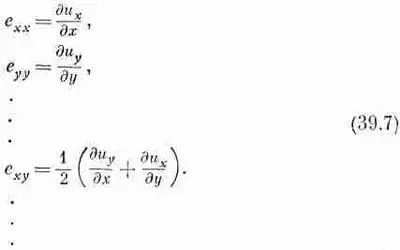

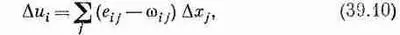
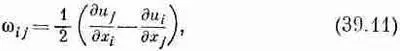



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
