Глава 39
УПРУГИЕ МАТЕРИАЛЫ
§ 1. Тензор деформации
§ 2. Тензор упругости
§ З. Движения в упругом теле
§ 4. Неупругое поведение
§ 5. Вычисление упругих постоянных
§ 1. Тензор деформации
В предыдущей главе мы говорили о возмущениях упругих тел в простых случаях. В этой главе мы посмотрим, что может происходить внутри упругого материала в общем случае. Как описать условия напряжения и деформации в большом куске желе, скрученном и сжатом каким-то очень сложным образом? Для этого необходимо описать локальную деформацию в каждой точке упругого тела, а это можно сделать, задав в ней набор шести чисел — компонент симметричного тензора. Ранее (в гл. 31) мы говорили о тензоре напряжений, теперь же нам потребуется тензор деформации.
Предположим, что мы взяли недеформированный материал и, прикладывая напряжение, наблюдаем за движением маленького пятнышка примеси, попавшей внутрь. Пятнышко, которое вначале находилось в точке Р и имело положение г=(x, у, z), передвигается в новую точку Р', т. е. в положение r'= (х', у', z'), как это показано на фиг. 39.1.
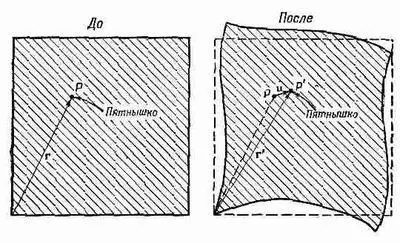
Фиг. 39.1. Пятнышко примеси в материале из точки Р недеформированного кубика после деформации перемещается в точку Р'.
Мы будем обозначать через и вектор перемещения из точки Р в точку Р', т. е.
u = r'-r.(39.1)
Перемещение и зависит, конечно, от точки Р, из которой оно выходит так, что и есть векторная функция от г или от (х, у, z).
Сначала рассмотрим простейший случай, когда деформация по всему материалу постоянна, т. е. то, что называется однородной деформацией. Предположим, например, что мы взяли балку из какого-то материала и равномерно ее растянули. Иначе говоря, мы просто равномерно изменили ее размер в одном направлении, скажем в направлении оси х (фиг. 39.2).
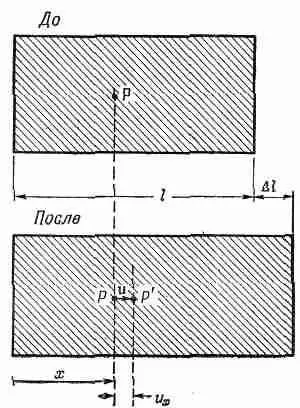
Фиг. 39.2. Однородная деформация растяжения.
Перемещение u x пятнышка с координатой х пропорционально самому х.
Действительно,
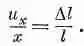
Мы будем записывать u x следующим образом:
и x =е хх х.
Разумеется, константа пропорциональности е хх — это то же, что наше старое отношение Dl/l. (Скоро вы увидите, почему нам потребовался двойной индекс.)
Если же деформация неоднородна, то связь между х и u x в материале будет изменяться от точки к точке. В таком общем случае мы определим е хх как своего рода локальную величину Dl/l, т. е.

Это число, которое теперь будет функцией х, у и z, описывает величину растяжения в направлении оси х по всему куску желе. Возможны, конечно, растяжения и в направлении осей у и z. Мы будем описывать их величинами
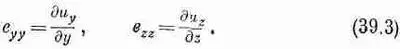
Кроме того, нам нужно описать деформации типа сдвигов. Вообразите, что в первоначально невозмущенном желе вы выделили маленький кубик. Нажав на желе, мы изменяем его форму, и наш кубик может превратиться в параллелограмм (фиг. 39.3).
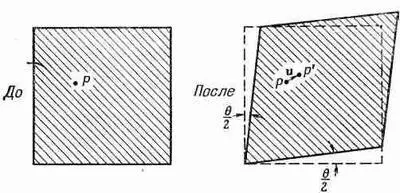
Фиг. 39.3. Однородная деформация сдвига.
При такой деформации перемещение в направлении х каждой частицы пропорционально ее координате у:

а перемещение в направлении у пропорционально х:
u y=(q/2)x. (39.5)
Таким образом, деформацию сдвигового типа можно описать с помощью
u x=e xy y u у =e yx x,
Читать дальше



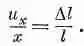

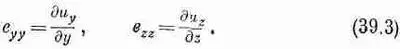





![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)
![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)
