Для анализа такого контакта я обозначу амплитуду того, что электрон окажется на одной стороне, через ψ 1, а того, что на другой,— через ψ 2. В сверхпроводящем состоянии волновая функция ψ 1— это общая волновая функция всех электронов с одной стороны, а ψ 2— соответствующая функция с другой стороны. Эту задачу можно решать для сверхпроводников разного сорта, но мы ограничимся самым простым случаем, когда вещество по обе стороны одно и то же, — так что соединение самое простое и симметричное. И пусть пока никакого магнитного поля нет. Тогда связь между этими двумя амплитудами должна быть такой:
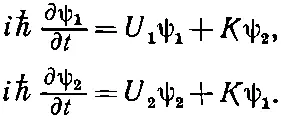
Постоянная К характеризует данный переход. Если бы К была равна нулю, то эта пара уравнений попросту описывала бы наинизшее энергетическое состояние (с энергией U ) каждого сверхпроводника. Но обе стороны связаны амплитудой К , выражающей возможность утечки из одной стороны в другую (это как раз известная нам по двухуровневым системам амплитуда «переброса»). Если обе стороны одинаковы, то U 1будет равно U 2, и я имею право их просто вычесть. Но теперь предположим, что мы подсоединили две сверхпроводящие области к двум полюсам батарейки, так что к переходу оказалась приложенной разность потенциалов V . Тогда U 1- U 2= qV . Для удобства я могу выбрать нуль энергии посредине между U 1и U 2, и тогда уравнения обратятся в
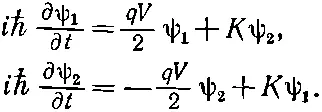 (19.40)
(19.40)
Это стандартные уравнения двух связанных квантовомеханических состояний. На этот раз давайте проанализируем их по-иному. Сделаем подстановки:
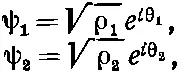 (19.41)
(19.41)
где θ 1и θ 2— фазы по обе стороны контакта, а ρ 1и ρ 2— плотности электронов в этих двух точках. Вспомним, что на практике ρ 1и ρ 2почти точно совпадают друг с другом и равны ρ 0— нормальной плотности электронов в сверхпроводящем материале. Если вы теперь подставите эти формулы для ψ 1и ψ 2в (19.40) и приравняете вещественные части вещественным, а мнимые — мнимым, то получится четверка уравнений (для краткости обозначено θ 2-θ 1=δ):
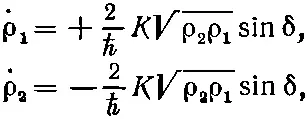 (19.42)
(19.42)
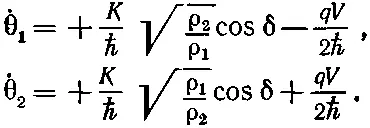 (19.43)
(19.43)
Первая пара уравнений говорит, что ρ 1=-ρ 2«Но,— скажете вы,— они ведь обе должны быть равны нулю, раз ρ 1и ρ 2обе постоянны и равны ρ 0». Не совсем. Эти уравнения описывают не все. Они говорят, какими были бы ρ 1и ρ 2, если бы не было добавочных электрических сил за счет того, что нет баланса между электронной жидкостью и фоном положительных ионов. Они сообщают, как начали бы меняться плотности, и поэтому описывают тот ток, который начал бы течь. Этот ток, текущий от стороны 1 к стороне 2, был бы как раз равен ρ 1(или -ρ 2), или
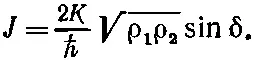 (19.44)
(19.44)
Такой ток вскоре зарядил бы сторону 2, если можно было бы забыть , что обе стороны соединены проводами с батареей. Однако он не зарядит область 2 (и не разрядит область 1), потому что возникнут токи, которые выровняют потенциал. В наши уравнения эти токи от батареи не входят. Если бы их добавить, то ρ 1и ρ 2оставались бы фактически постоянными, а ток через переход определялся бы формулой (19.44).
Поскольку ρ 1и ρ 2действительно остаются постоянными и равными ρ 0, давайте положим 2 K ρ 0/ ℏ = J 0и напишем
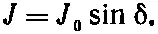 (19.45)
(19.45)
Тогда J 0, подобно К , есть число, характеризующее данный переход.
Другая пара уравнений (19.43) дает нам θ 1и θ 2. Нас интересует разность δ=θ 2-θ 1, которую мы хотим подставить в (19.45); из уравнений же мы имеем
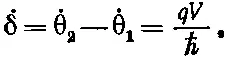 (19.46)
(19.46)
Это значит, что можно написать
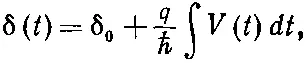 (19.47)
(19.47)
где δ 0— значение δ при t =0. Не забывайте также, что q — это заряд пары, q =2 q e . В уравнениях (19.45) и (19.47) содержится важный результат — общая теория переходов Джозефсона.
Читать дальше

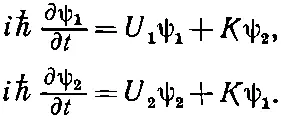
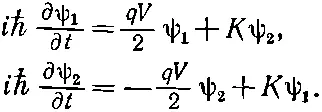 (19.40)
(19.40)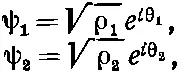 (19.41)
(19.41)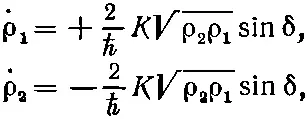 (19.42)
(19.42)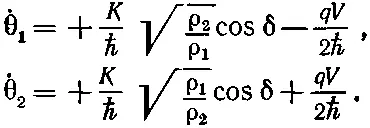 (19.43)
(19.43)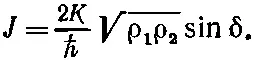 (19.44)
(19.44)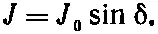 (19.45)
(19.45)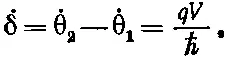 (19.46)
(19.46)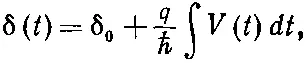 (19.47)
(19.47)


![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


