§ 1. Состояния молекулы аммиака
§ 2. Молекула в статическом электрическом поле
§ З. Переходы в поле, зависящем от времени
§ 4. Переходы при резонансе
§ 5. Переходы вне резонанса
§ 6. Поглощение света
§ 1. Состояния молекулы аммиака
В этой главе мы хотим обсудить применение квантовой механики в одном практическом устройстве — в аммиачном мазере. Вас может удивить, отчего это мы бросаем на полпути наше изложение формального аппарата квантовой механики и обращаемся к частной задаче. Но позже вы увидите, что многие черты этой частной задачи сплошь и рядом встречаются и в общей теории квантовой механики, так что детальное изучение задачи многому нас научит. Аммиачный мазер — это устройство для генерирования электромагнитных волн. Его действие основано на свойствах молекулы аммиака, о которых вкратце говорилось в предыдущей главе. Поэтому сначала мы подведем итоги тому, что нам уже известно.
Молекула аммиака имеет много состояний. Но мы будем считать ее системой с двумя состояниями (двухуровневой); сейчас нас интересует лишь то, что бывает, когда молекула находится в любом заданном состоянии вращения или поступательного движения. Физическую модель этих двух состояний можно наглядно представить себе следующим образом. Если вращать молекулу аммиака вокруг оси, проведенной через атом азота перпендикулярно плоскости атомов водорода, как показано на фиг. 7.1, мы обнаружим, что существуют два сорта состояний, которые не переходят друг в друга при таких поворотах и отличаются положением атома азота.
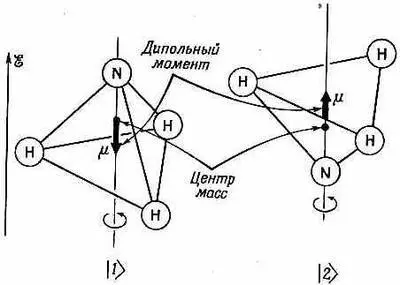
Фиг. 7.1. Физическая модель двух базисных состояний молекулы аммиака. Электрические дипольные моменты этих состояний равны m.
Азот может быть либо по одну сторону плоскости атомов водорода, либо по другую. Эти два состояния мы обозначаем |1> и |2>. Их мы выберем в качестве совокупности базисных состояний в нашем анализе поведения молекулы аммиака.
В системе с двумя базисными состояниями любое состояние |y> системы всегда может быть описано линейной комбинацией двух базисных состояний; это значит, что существует определенная амплитуда С 1быть в одном базисном состоянии и амплитуда С 2быть в другом. Вектор состояния |y>можно записать в виде
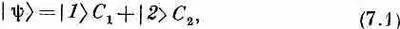
где
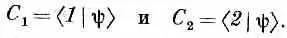
Эта пара амплитуд меняется со временем согласно нашим гамильтоновым уравнениям — уравнениям (6.43). Используя симметрию двух состояний молекулы аммиака, мы полагаем H 11 =H 22 =E 0и H 12= H 21=- А и получаем такое решение [см. (6.50) и (6.51)]:
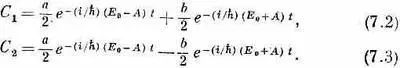
Кинем теперь на эти решения более внимательный взгляд. Пусть сперва молекула была поставлена в состояние |y 11>, для которого коэффициент b был равен нулю. Тогда при t =0 амплитуды оказаться в состояниях |1> и |2> одинаковы и останутся такими все время. Их фазы обе меняются во времени одинаково, с частотой ( E 0- A)/h. И точно так же, если бы мы поставили молекулу в состояние |y 1> , для которого а=0, амплитуда C 2равнялась бы C 1с минусом, и это соотношение сохранилось бы навсегда — обе амплитуды менялись бы теперь во времени с частотой (E 0 +A)/h. Это все состояния, для которых связь между С 1и С 2не зависит от времени; других возможностей нет.
Мы нашли два частных решения, в которых амплитуды не меняются по величине и, более того, фазы меняются с одинаковой частотой. Это стационарные состояния по определению, данному в гл. 5, § 1, т. е. состояния с определенной энергией. Состояние |y 11> обладает энергией Е 11= Е 0- А, а состояние |y 1> — энергией E 1 =E 0 +A. Кроме этих, никаких стационарных состояний не существует, т. е. мы обнаруживаем, что у молекулы есть два уровня энергии, отличающиеся на 2А. (Подразумеваются, конечно, два уровня энергии для заданного состояния колебания и вращения, о которых говорилось в наших исходных допущениях.)
Читать дальше


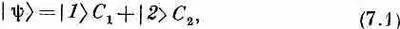



![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


