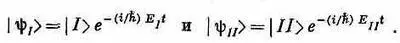
У этих состояний С 1и С 2будут даваться уравнениями (7.18) и (7.19), где а 1и а 2еще подлежат определению. Их отношение дается либо формулой (7.23), либо (7.24). Они должны также удовлетворять еще одному условию. Если известно, что система находится в одном из стационарных состояний, то сумма вероятностей того, что она окажется в |1 >или | 2 >, должна равняться единице. Следовательно,

или, что то же самое,

Эти условия не определяют а 1и а 2однозначно: остается еще произвол в фазе, т. е. в множителе типа е i d . Хотя для а можно выписать общие решения, но обычно удобнее вычислять их в каждом отдельном случае.
Вернемся теперь к нашему частному примеру молекулы аммиака в электрическом поле. Пользуясь значениями Н 11 , H 22и Н 12из (7.14) и (7.15), мы получим для энергий двух стационарных состояний выражения
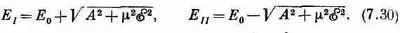
Эти две энергии как функции напряженности x электрического поля изображены на фиг. 7.2.
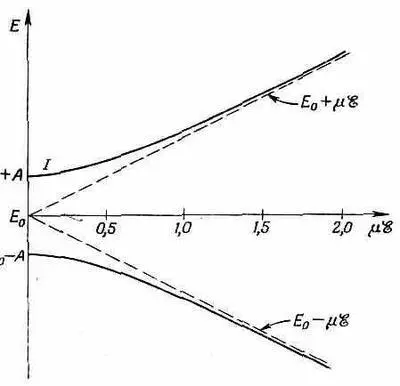
Фиг. 7,2. Уровни энергии молекулы аммиака в электрическом поле.
Кривые построены по формулам (7.30): 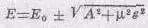
Когда электрическое поле нуль, то энергии, естественно, обращаются в Е 0 ±А. При наложении электрического поля расщепление уровней растет. Сперва при малых x оно растет медленно, но затем может стать пропорциональным $. (Эта линия — гипербола.) В сверхсильных полях энергии попросту равны
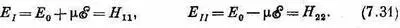
Тот факт, что у азота существует амплитуда переброса вверх — вниз, малосуществен, когда энергии в этих двух положениях сильно отличаются. Это интересный момент, к которому мы позже еще вернемся.
Теперь мы наконец готовы понять действие аммиачного мазера. Идея в следующем. Во-первых, мы находим способ отделения молекул в состоянии | I > от молекул в состоянии | II >. Затем молекулы в высшем энергетическом состоянии | I > пропускаются через полость, у которой резонансная частота равна 24000 Мгц. Молекулы могут оставить свою энергию полости (способ будет изложен позже) и покинуть полость в состоянии | II >. Каждая молекула, совершившая такой переход, передаст полости энергию E=E I -Е II . Энергия, отобранная у молекул, проявится в виде электрической энергии полости.
Как же разделить два молекулярных состояния? Один способ такой. Аммиачный газ выпускается тонкой струйкой и проходит через пару щелей, создающих узкий пучок (фиг. 7.3).
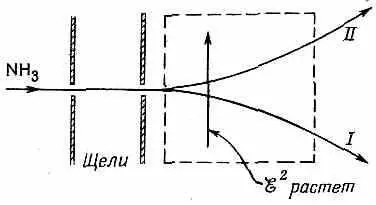
Фиг. 7.3. Пучок молекул аммиака может быть разделен электрическим полем, в котором x 2 обладает градиентом, перпендикулярным пучку.
Затем пучок пропускается через область, в которой имеется сильное поперечное электрическое поле. Создающие поле электроды изогнуты так, чтобы электрическое поле поперек пучка резко менялось. Тогда квадрат x·x электрического поля будет иметь большой градиент, перпендикулярный пучку. А у молекулы в состоянии |/> энергия с x 2растет, значит, эта часть пучка отклонится в область меньших x 2. Молекула же в состоянии | II >, наоборот, отклонится к области, где x 2побольше, потому что ее энергия падает, когда x 2растет.
Кстати, при тех электрических полях, которые удается генерировать в лаборатории, энергия m x всегда много меньше А. В этом случае корень в уравнении (7.30) приближенно равен

Во всех практических случаях энергетические уровни, стало быть, равны
Читать дальше

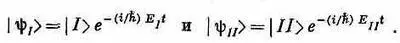


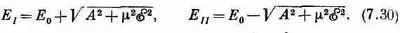

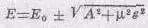
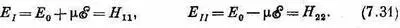





![Ричард Фейнман - Фейнмановские лекции по физике. Современная наука о природе [litres]](/books/398001/richard-fejnman-fejnmanovskie-lekcii-po-fizike-sov-thumb.webp)

![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


