Так что же из них следует? Сначала приложим постоянное напряжение. Если приложить постоянное напряжение V 0, то аргумент синуса примет вид δ 0+( q / ℏ ) V 0 t . Поскольку ℏ/ q —число маленькое (по сравнению с обычными напряжениями и временами), то синус будет колебаться довольно быстро и в итоге никакой ток не пойдет. (Практически, поскольку температура не равна нулю, небольшой ток все же будет из-за проводимости «нормальных» электронов.) С другой стороны, если напряжение на переходе равно нулю , то ток может пойти! Если нет напряжения, то ток может равняться любой величине между + J 0и - J 0(в зависимости от того, каково значение δ 0). Но попробуйте приложить напряжение — и ток обратится в нуль. Это странное поведение недавно наблюдалось экспериментально [101] P. W. Andеrsоn, J. M. Роwеll, Phys. Rev. Letters, 10, 230 (1963).
.
Ток можно получить и другим способом: кроме постоянного напряжения — приложить еще и высокую частоту. Пусть
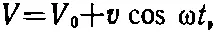
где v ≪ V . Тогда
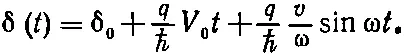
Но при малых Δ x
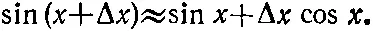
Разложив по этому правилу sinδ, я получу
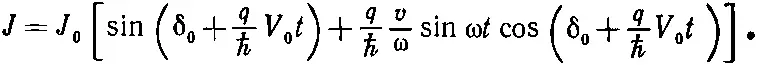
Первый член в среднем дает нуль, но второй в нуль не обращается, если
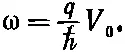
Значит, если частота переменного напряжения равна ( q / ℏ ) V 0, то через контакт пойдет ток. Шапиро [102] S. Shapirо, Phys. Rev. Letters, 11, 80 (1963).
сообщил, что он наблюдал такой резонансный эффект.
Если вы просмотрите работы на эту тему, то заметите, что в них формула для тока часто записывается в виде
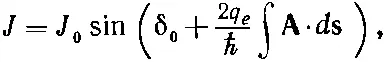 (19.48)
(19.48)
где интеграл берется по пути, ведущему через переход. Причина здесь в том, что если переход находится в поле векторного потенциала, то фаза амплитуды переброса видоизменяется так, как было объяснено вначале [уравнение (19.1)]. Если вы всюду включите такой сдвиг фазы, то получите нужные формулы.
Наконец, я хотел бы описать очень эффектный и интересный опыт по интерференции токов, проходящих через два перехода, который был недавно проделан. Мы привыкли встречаться в квантовой механике с интерференцией амплитуд от двух щелей. Сейчас мы будем иметь дело с интерференцией двух токов, текущих через два перехода между сверхпроводниками. Она вызывается различием в фазах, с которыми сливаются токи, прошедшие по двум разным путям. На фиг. 19.7 показано параллельное соединение двух переходов а и b между сверхпроводниками.
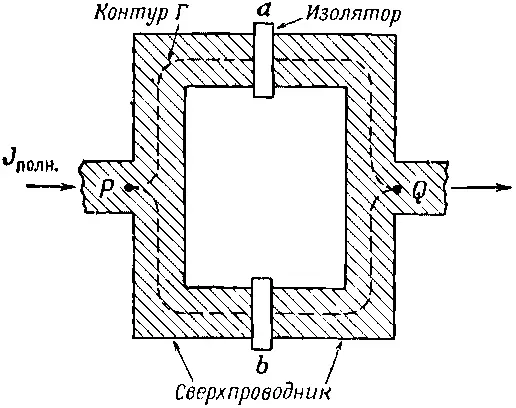
Фиг. 19.7. Два параллельных перехода Джозефсона.
Концы сверхпроводников Р и Q подключены к приборам, которыми мы измеряем ток. Внешний ток J полнбудет суммой токов через каждый из переходов. Пусть J a и J b это токи через переходы, и пусть их фазы будут δ а и δ b . Разность фаз волновых функций в точках Р и Q должна быть одинаковой, по какому бы пути вы ни пошли. На том пути, который следует через переход а , разность фаз между Р и Q равна δ а плюс криволинейный интеграл от векторного потенциала вдоль верхнего пути:
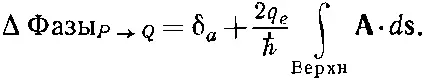 (19.49)
(19.49)
Почему? Потому что фаза θ связана с Ауравнением (19.26). Если вы это уравнение проинтегрируете вдоль какого-то пути, то левая часть даст изменение фазы, которое тем самым как раз окажется пропорциональным криволинейному интегралу от А, что и написано. Изменение фазы по нижнему пути может быть записано подобным же образом:
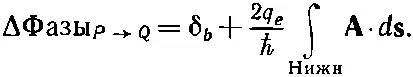 (19.50)
(19.50)
Эти величины должны быть равны; если я их вычту, то получу, что разность дельт должна быть равна контурному интегралу от Апо замкнутому пути
Читать дальше

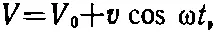
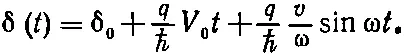
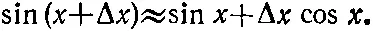
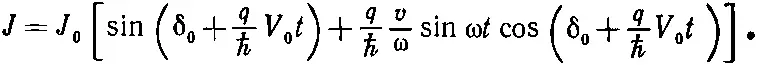
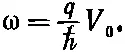
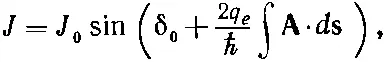 (19.48)
(19.48)
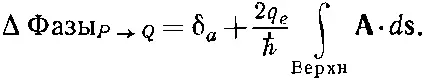 (19.49)
(19.49)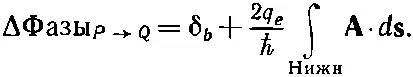 (19.50)
(19.50)


![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


