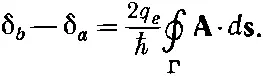
Здесь интеграл берется по замкнутому контуру Г (см. фиг. 19.7), проходящему через оба перехода. Интеграл от Аэто магнитный поток Ф через контур. Итак, две дельты оказываются отличающимися на 2 q e / ℏ , умноженное на магнитный поток Ф, который проходит между двумя ветвями схемы:
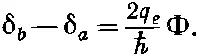 (19.51)
(19.51)
Изменяя магнитное поле в схеме, я смогу контролировать эту разность фаз. Я ее прилажу так, чтобы посмотреть, проявится ли в полном токе, текущем сквозь оба перехода, интерференция между его частями. Полный ток равен сумме J a и J b . Для удобства я приму
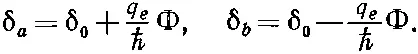
Тогда
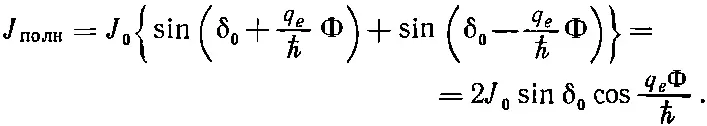 (19.52)
(19.52)
Мы не знаем, каково значение δ 0, и природа здесь может, в зависимости от обстоятельств, вытворять все, что ей заблагорассудится. В частности, δ 0может зависеть от прилагаемого к переходам внешнего напряжения. Но что бы мы ни делали, sinδ 0не окажется больше единицы. Значит, предельно сильный ток для каждого данного Ф дается формулой
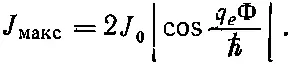
Этот предельный ток меняется, смотря по тому, каково Ф, и сам достигает максимума всякий раз, когда
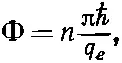
где n — целое число. Иными словами, ток достигает своего максимума, когда зацепляющийся за схему поток принимает те самые квантованные значения, которые мы получили в уравнении (19.30)!
Ток Джозефсона через двойной переход недавно был измерен [103] Jaklevic, Lambe, Silver, Mercereau, Phys. Rev. Letters, 12, 159 (1964).
как функция магнитного поля в области между ветвями. Результаты приведены на фиг. 19.8.
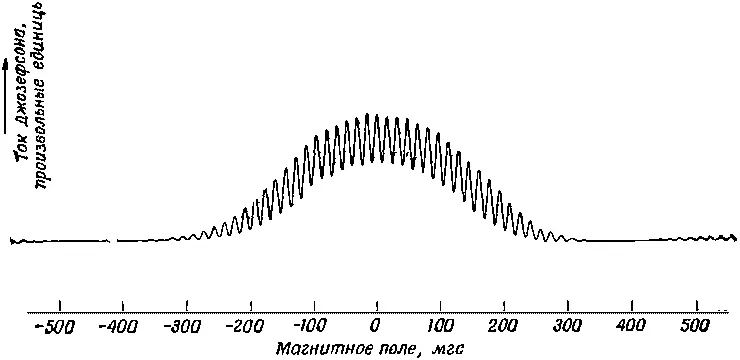
Фиг. 19.8. Запись тока через два параллельных перехода Джозефсона как функции магнитного поля в области между двумя переходами.
Здесь мы видим общий фон от токов, вызываемых различными эффектами, которыми мы пренебрегли, но быстрые колебания тока при изменении магнитного поля объясняются наличием интерференционного члена cos ( q e Ф / ℏ ) в (19.52).
Один из самых интригующих вопросов квантовой механики— это вопрос о том, существует ли векторный потенциал в том месте, где нет поля [104] Jaklevic, Lambe, Silver, Mercereau, Phys. Rev. Letters, 12, 274 (1964).
. Опыт, который я только что описал, был проделан тоже с узеньким соленоидом, помещенным между двумя переходами, так что заметное магнитное поле Вбыло только внутри соленоида, а на сверхпроводящие провода его попадало пренебрежимо мало. И вот оказалось, что сила тока колеблется с изменением потока магнитного поля внутри этого соленоида, даже если само поле и не касается проводов. Это еще одно доказательство «физической реальности» векторного потенциала [см. гл. 15, § 5 (вып. 6)].
Я не знаю, что теперь на очереди. Но посмотрите-ка, что можно было бы сделать. Во-первых, заметьте, что интерференция между двумя переходами может быть применена для создания чувствительного магнитометра. Если площадь, охватываемая двумя переходами, равна, скажем, 1 мм 2, то максимумы на кривой фиг. 19.8 будут отстоять друг от друга на 2·10 -5 гс . Одну десятую промежутка между пиками запросто можно заметить; значит, таким соединением можно будет измерять поля величиной в 2·10 -6 гс , или замерять большие поля со столь же хорошей точностью. Можно даже пойти дальше. Представим, например, что мы вплотную друг к другу на равных расстояниях расставили 10—20 переходов. Тогда получится интерференция на 10—20 щелях, и при изменении магнитного поля мы получим очень резкие максимумы и минимумы. Вместо интерференции на двух щелях у нас будет двадцати-, а может быть, и стощелевой интерферометр для измерения магнитного поля. Вероятно, можно предсказать, что измерения магнитных полей при использовании квантовомеханической интерференции станут почти такими же точными, как измерения длин световых волн.
Читать дальше

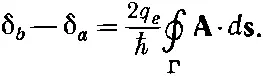
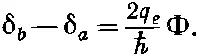 (19.51)
(19.51)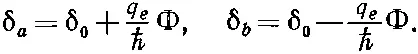
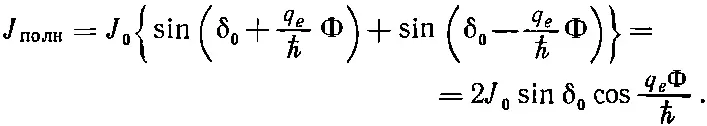 (19.52)
(19.52)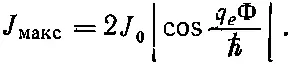
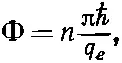




![Пол Халперн - Квантовый лабиринт. Как Ричард Фейнман и Джон Уилер изменили время и реальность [litres]](/books/414310/pol-halpern-kvantovyj-labirint-kak-richard-fejnman-thumb.webp)


