Ричард Фейнман - Том 3. Квантовая механика

Сказанное нами может вас слегка ввести в заблуждение. Поглощение ультрафиолетового света в принятой нами для бензола системе с двумя состояниями было бы очень слабым, потому что матричный элемент дипольного момента между двумя состояниями равен нулю. [Оба состояния электрически симметричны, и в нашей формуле (7.55) для вероятности перехода дипольный момент μ равен нулю, и свет не поглощается.] Если бы других состояний не было, существование верхнего состояния пришлось бы доказывать иными путями. Однако более полная теория бензола, которая исходит из большего числа базисных состояний (обладающих, скажем, смежными двойными связями), показывает, что истинные стационарные состояния бензола слегка искажены по сравнению с найденными нами. В результате все же возникает дипольный момент, который и разрешает упомянутые в тексте переходы, приводящие к поглощению ультрафиолетового света.

Мы принимаем энергию покоя m 0c 2за «нуль» энергии и считаем магнитный момент μ электрона отрицательным числом, поскольку он направлен против спина.

Параграф 5 при первом чтении книги можно пропустить. Он сложнее, чем положено в таких курсах.

Это похоже на то, что мы обнаружили (в гл. 4) для частиц со спином 1/ 2, когда поворачивали систему координат вокруг оси z; тогда мы получили фазовые множители exp (±iφ/2). В действительности это в точности то же самое, что мы писали в гл. 3, § 7, для состояний |+> и |-> частицы со спином 1, и это не случайно. Фотон— это частица со спином 1, у которой, однако, нет «нуль»-состояния.

Мы сознаем, что материал этого параграфа длиннее и труднее, чем это положено на нашем уровне знаний. Лучше пропустите его и переходите прямо к § 6. Но если у вас есть самолюбие и время, попозже вернитесь к нему опять. Это великолепнейший пример (взятый к тому же из последних работ по физике высоких энергий) того, что можно сотворить с помощью нашей формулировки квантовой механики двухуровневых систем. (Для русского издания параграф переделан проф. Сэндсом. — Прим. ред.)

Читайте: «.K-нуль с чертой».

Среди новых частиц есть барион Ω -со странностью -3.—Прим. ред.

Если, конечно, он не создает еще двух К +или других частиц с общей странностью +2. Можно считать, что здесь речь идет о реакциях, в которых не хватает энергии для возникновения этих добавочных странных частиц.

Свободная Λ-частица медленно распадается путем слабого взаимодействия (так что странность не обязана при этом сохраняться). Продуктами распада могут быть либо р и π -, либо n и π 0. Время жизни 2,2·10 -10сек.

Типичное время для сильного взаимодействия ближе к 10 -23сек.

Мы здесь упрощаем. Система 2π может иметь множество состояний, отвечающих различным импульсам π-мезонов, и в правой части этого равенства следовало бы поставить сумму по всем базисным состояниям π-мезонов. Но полный вывод все равно приводит к тем же результатам.

Такую интерференцию действительно наблюдали. Коэффициент α оказался равным — 0,96β. Отсюда можно было вычислить и разность масс К 1- и K 2-мезонов. Она оказалась равной около —0,35·10 -5эв. Это наименьшая разность масс двух частиц, известных физикам.— Прим. ред.

Для этих операторов, правда, оказывается, что от их порядка ничего не зависит.

Этот оператор сейчас называют оператор обмена спинами.

В действительности состоянием является

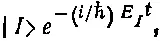
но, как обычно, мы отождествим состояния с постоянными векторами, которые при t=0 совпадают с настоящими векторами.

Crampton, Kleppner, Ramsey, Physical Review Letters, 11, 338 (1963).

Вспомните, что классически U=- μ· B, так что энергия наименьшая, когда момент направлен по полю. Для положительно заряженных частиц магнитный момент параллелен спину, для отрицательных — наоборот. Значит, в (10.27) μ р— число положительное, а μ е— отрицательное.

Тем, кто перескочил через гл. 4, придется пропустить и этот параграф.