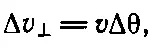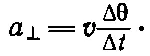Чтобы записать законы Ньютона в векторной форме, мы должны поучиться еще кое-чему и определить вектор ускорения. Этот вектор равен производной по времени вектора скорости, причем легко показать, что его составляющие равны вторым производным x, y и z по t :
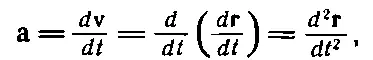 (11.11)
(11.11)
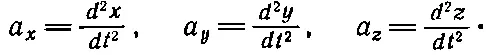 (11.12)
(11.12)
После этого законы Ньютона можно записать таким образом:
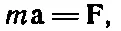 (11.13)
(11.13)
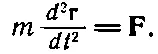 (11.14)
(11.14)
Теперь задача о доказательстве инвариантности законов Ньютона относительно вращений сводится к следующему: нужно доказать, что а (ускорение) есть вектор; это мы уже сделали. Затем нужно доказать, что F(сила) есть вектор; это мы предполагаем . Следовательно, если сила есть вектор, то уравнение (11.13) будет выглядеть одинаково во всех системах координат, ибо нам известно, что ускорение тоже вектор. Запись уравнений в виде, не содержащем явно x, y, z , привлекательна тем, что нам нет необходимости выписывать три уравнения каждый раз, когда мы хотим написать законы Ньютона или другие законы физики. Мы записываем то, что выглядит как один закон, хотя фактически, конечно, это три закона для каждой оси системы координат, потому что любое векторное уравнение содержит в себе утверждение, что все составляющие равны .
Тот факт, что ускорение — это скорость изменения вектора скорости, помогает найти ускорение в любых, казалось бы, трудных обстоятельствах. Предположим, например, что частица, двигаясь по какой-то сложной кривой (фиг. 11.7), имеет в момент t 1скорость v 1, а несколько позже, в момент t 2,скорость v 2.
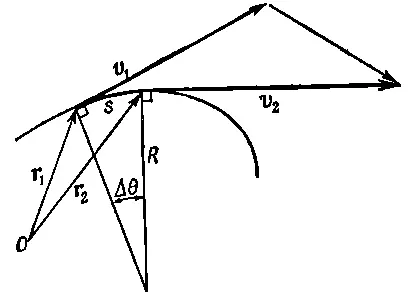
Фиг. 11 .7. Криволинейная траектория.
Чему равно ускорение? Ответ : ускорение равно разности скоростей, деленной на малый промежуток времени; значит, нужно знать разность скоростей. Как же найти эту разность? Чтобы найти разность двух векторов, проведем вектор через концы векторов v 2и v 1, иначе говоря, начертим вектор Δ в качестве разности этих двух векторов. Верно? Нет ! Мы можем поступать так только тогда, когда начала векторов расположены в одной точке! Вычитать векторы, приложенные к разным точкам, бессмысленно. Остерегайтесь этого! Чтобы вычесть векторы, нужно начертить другую схему. На фиг. 11. 8 векторы v 1и v 2перенесены параллельно и равны их двойникам, изображенным на фиг. 11.7.
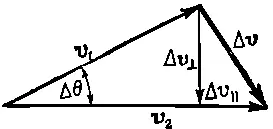
Фиг. 11.8. Диаграмма для вычисления ускорения.
Теперь можно поговорить об ускорении. Ускорение, конечно, просто равно Δ v/Δ t . Интересно заметить, что разность скоростей можно разделить на две части: можно представить себе, что ускорение состоит из двух составляющих : Δ v ║—вектора, параллельного касательной к пути, и вектора Δ v ┴, перпендикулярного к этой касательной. Эти векторы показаны на фиг. 11.8. Касательное к пути ускорение равно, естественно, лишь изменению длины вектора, т. е. изменению величины скорости v :
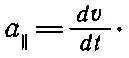 (11.15)
(11.15)
Другую, поперечную составляющую ускорения легко вычислить, взглянув на фиг. 11.7 и 11.8. За короткое время Δ t изменение угла между v 1и v 2равно малому углу Δθ. Если величина скорости равна v , то
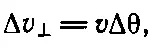
а ускорение а равно
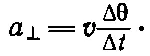
Теперь нам нужно знать Δθ/Δ t . Эту величину можно найти так: если в данный момент кривую можно приблизительно заменить окружностью радиусом R , то, поскольку за время Δ t частица пройдет расстояние s = v Δ t , изменение угла равно
Читать дальше

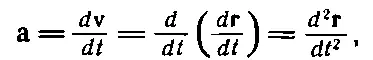 (11.11)
(11.11)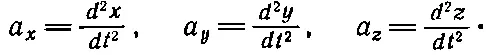 (11.12)
(11.12)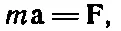 (11.13)
(11.13)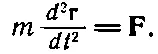 (11.14)
(11.14)

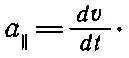 (11.15)
(11.15)