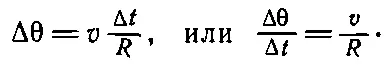
Таким образом, как мы уже установили ранее,
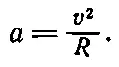 (11.16)
(11.16)
§ 7. Скалярное произведение векторов
Давайте еще немного займемся свойствами векторов. Легко понять, что длина шага в пространстве одинакова во всех координатных системах. Следовательно, если какому-то шагу r соответствуют составляющие x, y, z в одной системе координат и составляющие х ', у ', z ' в другой системе, то расстояние r=|r| одно и то же в обеих системах. Сначала мы, конечно, должны ввести два расстояния,
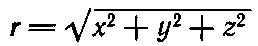
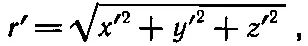
а затем проверить, что эти обе величины равны. Чтобы не возиться с квадратным корнем, будем сравнивать квадраты расстояний. Мы должны, таким образом, показать, что
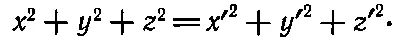 (11.17)
(11.17)
Подставив в это уравнение определяемые соотношением (11.5) значения x ', у ', z ', мы увидим, что это действительно так. Значит, кроме уже изученных нами векторных уравнений, существуют еще какие-то соотношения, верные в любой системе координат.
Незаметно мы получили новый тип величин. Мы можем построить функцию x, y и z , называемую скалярной функцией , — величину, которая не имеет направления, и одинакова в обеих системах координат. Из вектора можно построить скаляр. Хорошо бы найти общее правило для этого построения. Собственно говоря, мы уже нашли это правило: надо возвести в квадрат каждую из составляющих вектора и сложить их. Определим теперь новую величину, которую обозначим а· а. Это не вектор, а скаляр; это число, одинаковое во всех координатных системах и определяемое как сумма квадратов трех составляющих вектора:
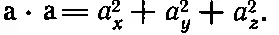 (11.18)
(11.18)
Вы спросите: «В какой системе координат?» Но раз это число не зависит от системы координат, то ответ одинаков в любой системе координат. Мы имеем дело с новым видом величины, с инвариантом , или скаляром , полученным «возведением вектора в квадрат». Если теперь определить, исходя из векторов аи b, величину
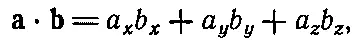 (11.19)
(11.19)
то можно убедиться, что эта величина совпадает в штрихованной и нештрихованной системах координат. Чтобы доказать это, заметим, что это верно для величин a· a, b· bи c· c,где c=a+b.Сумма квадратов ( a x + b x ) 2+( a y + b y ) 2+( a z + b z ) 2— инвариант:
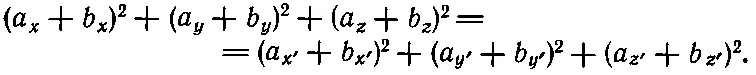 (11.20)
(11.20)
Раскроем скобки в обеих сторонах этого уравнения. Перекрестные произведения дадут нам выражения типа (11.19), а суммы квадратов составляющих аи b— выражения (11.18). Инвариантность слагаемых типа (11.18) приводит к инвариантности перекрестных произведений типа (11.19).
Величина а· bназывается скалярным произведением двух векторов аи bи имеет много интересных и полезных свойств. Например, легко доказать, что
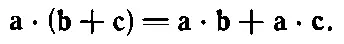 (11.21)
(11.21)
Есть еще очень простой геометрический способ вычисления а· b,при котором не надо определять составляющих аи b; просто а· bесть произведение длин векторов аи bна косинус угла между ними. Почему? Предположим, что мы выбрали такую систему координат, в которой вектор а направлен вдоль оси х ; в этом случае вектор аимеет единственную ненулевую составляющую а x , которая равна длине вектора а. Таким образом, уравнение (11.19) сводится в этом случае к a · b = a x b x , что равно произведению длины вектора ана составляющую вектора bпо направлению а, которая в свою очередь равна b cosθ, т. е.
Читать дальше

 (11.16)
(11.16)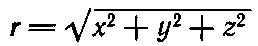
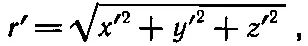
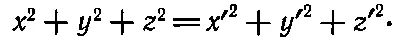 (11.17)
(11.17)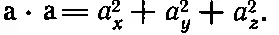 (11.18)
(11.18)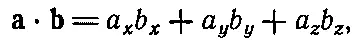 (11.19)
(11.19)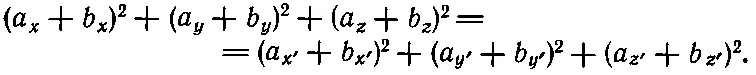 (11.20)
(11.20)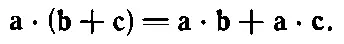 (11.21)
(11.21)




