Ричард Фейнман - Том 1. Механика, излучение и теплота

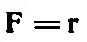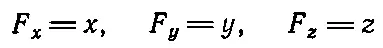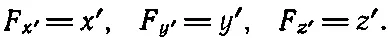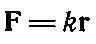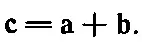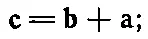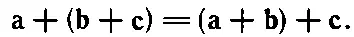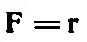
справедливо в любой системе координат, если оно верно хотя бы в одной из них. Оно заменяет нам три уравнения

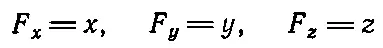
или соответственно

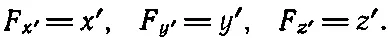
Тот факт, что физические соотношения между какими-либо величинами можно выразить в виде векторных уравнений, говорит о том, что эти соотношения верны в любой системе координат. Вот почему понятие вектора очень удобно в физике.

Давайте теперь рассмотрим некоторые свойства векторов. В качестве примера «вектора» можно указать скорость, импульс, силу и ускорение. Часто бывает удобно изобразить вектор в виде стрелки, указывающей направление действия. Но почему же можно представить силу стрелкой? Да потому, что она преобразуется по тем же законам, что и «шаг в пространстве». Именно поэтому можно представить силу в виде чертежа, как если бы это изображалось перемещение, причем выберем такой масштаб, чтобы единица силы, например ньютон, соответствовала некоторой длине. Проделав такую процедуру однажды, мы всегда сможем изображать силы в виде отрезков, потому что уравнение типа

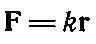
(где k — некоторая постоянная) имеет вполне определенный смысл. Возможность представлять силу отрезком сулит нам большие выгоды, потому что, изобразив отрезок или стрелку, можно не заботиться о координатных осях. При этом, конечно, всегда можно быстро подсчитать, как изменяются составляющие вектора при поворотах осей, потому что дело сводится к простому геометрическому построению.

Теперь мы должны описать законы, или правила, регулирующие возможные сочетания различных векторов. Прежде всего мы изучим сумму двух векторов. Пусть векторы aи bзадаются в какой-нибудь системе координат составляющими а x , a y , a z и b x , b y , b z . Предположим, что кому-то пришло в голову составить три числа а x + b x , a y + b y , а z + b z . Получим ли мы в результате вектор? Вы можете сказать: «Разумеется, ведь это три числа, а три числа образуют вектор». Нет, вектор образуют не любые три числа! Чтобы задать вектор, мы должны связать заданные нам три числа с координатной системой так, чтобы при повороте координатных осей эти числа «поворачивались» относительно друг друга и «перемешивались» по описанным ранее правилам. Таким образом, мы должны выяснить, во что превращаются числа а x + b x , а y + b y , a z + b z , если известно, что при изменении системы координат числа а x , а у , a z переходят в а ' x , а ' у , a ' z , а b x , b у , b z переходят в b ' x , b ' y , b ' z? Получим ли мы после поворота координатных осей числа а ' x + b ' x , a ' y + b ' y , a ' z + b ' z ? Ответ, конечно, будет утвердительным, потому что наше основное уравнение (11 :5) определяет так называемое линейное преобразование. Если мы применим это преобразование к а x и b x и вычислим а x + b x то окажется, что преобразованное а x + b x есть то же самое, что и а x + b x . «Складывая» векторы аи bпо только что описанному правилу, мы получаем новый вектор c. Мы запишем это так:

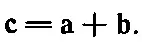
Вектор с обладает интересным свойством:

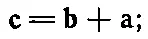
это легко проверить, написав составляющие вектора с. Кроме того,

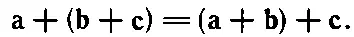
Векторы можно складывать в любом порядке.

Каков геометрический смысл a+ b? Как будет выглядеть вектор с, если мы, скажем, изобразим aи bс помощью стрелок? Ответ на этот вопрос дает фиг. 11.4.