Julian Barbour - The End of Time - The Next Revolution in Physics

There are only four freedoms that remain. Having placed the centre of mass of the second triangle at some position, we can change its orientation (three freedoms). We can also change the amount of Newton’s absolute time that elapses between the instants at which the three bodies occupy the two positions (one freedom, the fourth). If the time difference is shortened, this means that the bodies travel farther in less of Newton’s time – that is, they are moving faster initially. In fact, since the motion of the centre of mass does not matter, we can keep it fixed and change only the orientation. Now, at last, we come to something that does matter. Both these changes – in the time difference and in the relative orientation – have dramatic consequences, which are illustrated in Figures 13 and 14.

Figures 13 and 14 express the entire mystery of absolute space and time. Both of Newton’s absolutes are invisible, yet their effects show up in the evolutions of the triangles, which are more or less directly visible. The astronomers do see stars and the spaces between them (admittedly in projection) when they look through telescopes. If time were merely change and only distances had dynamical effect, a decent Machian mechanics – one that would satisfy Laplace’s divine intelligence – should lead to exactly the same evolutions in all nine cases. This is manifestly not true for the real triple-star systems that astronomers observe. All the different kinds of evolution shown in Figures 13 and 14, and many more, are found. All the facts that enabled Newton to win his argument against Leibniz are contained in these diagrams, but it took about two centuries before Poincaré found the best way to demonstrate them. He concluded regretfully that a mechanics that uses only relative quantities, as Mach advocated, cannot get off the ground. It lacks perfect Laplacian determinism. Nevertheless, the failure is curious. Absolute space and time could have had an effect through all the freedoms allowed in the placing of the two triangles. There are fourteen degrees of freedom in total, of which ten have no effect whatsoever. This is just what the invisibility of space and time would lead us to expect. Yet four degrees of freedom do have a profound influence. Three are associated with twists in space, the fourth with the overall speed put into the system. These strange mismatches between expectation and reality have kept the philosophers arguing and the physicists puzzling for centuries.

The fact is that Newton’s absolute space and time play a decidedly odd role. The first problem is their invisibility. The more serious problem is what little part they play in the whole story, and how irrationally they enter the stage when they do participate in the action. Once we have chosen the relative orientation and time separation of the two triangles, we can take them anywhere in absolute space and time. They will always give rise to the same evolution. Absolute space and time seem to matter very little; only the relative orientation and time separation count.

Figure 13.These are ‘spaghetti diagrams’ of evolutions in absolute space like the left-hand one in Figure 12 (the one at the top left is the same evolution but with the triangles removed). The corresponding curves in Shape Space are shown in Figure 14. In each diagram the evolution commences with the three bodies forming an equilateral triangle, and all the corresponding curves start in the same direction in Triangle Land and Shape Space. This is because the second triangle is the same in both cases. The different evolutions are created by giving the bodies different initial speeds (they are different in the three rows) and by giving the triangles different orientational twists (different in the three columns).

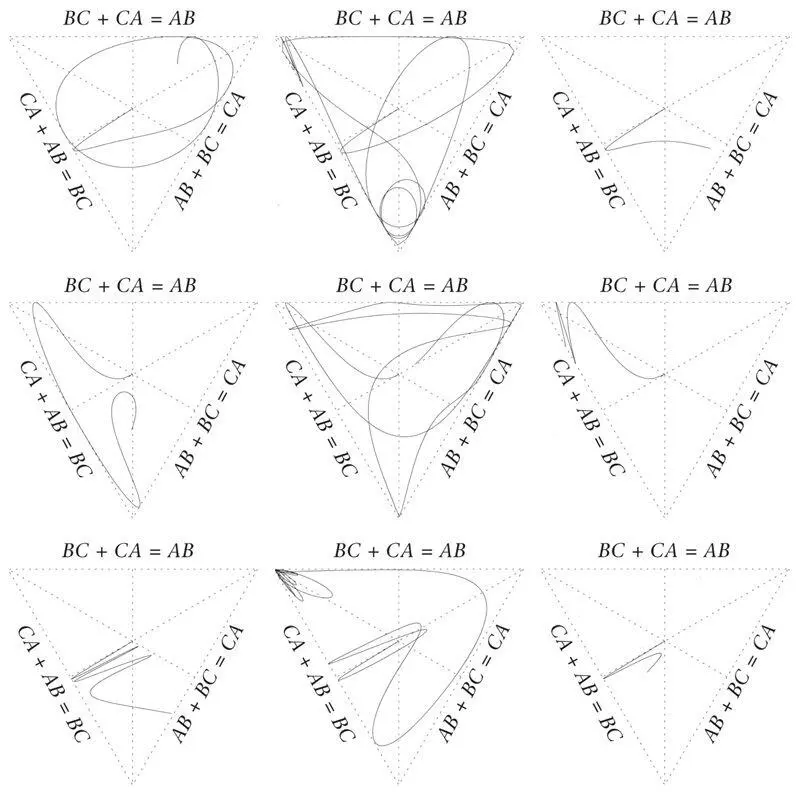
Figure 14.These are the curves in Shape Space corresponding to the nine evolutions in absolute space shown in Figure 13. They all start from the same point with the same direction, but then diverge strongly. Remember, as I explained in the caption to Figure 9, that these curves represent not the motion of a single particle across the page, but the shapes of continuous sequences of triangles. If you ‘stuck a pin’ into any point on one of these curves, the triangle corresponding to it would ‘light up’. It is very important to appreciate that Figures 13 and 14 show identical happenings in two different ways. Since Newton’s time, nearly all physicists have believed the Newtonian representation, Figure 13, to be the physically correct way to think about these things.

Following Leibniz and Mach, I believe Figure 14 is the right way. However, this approach faces a severe difficulty explained in the text. It is only in Chapter 7 that I shall explain how it is overcome.

But these are our arbitrary choices. Once we have chosen two triangles, nothing about the triangles in themselves gives any hint as to how we should make the choices. Leibniz formulated two great principles of philosophy that most scientists would adhere to. The first is the identity of indiscernibles: if two things are identical in all their attributes, then they are actually one. They are the same thing. The second, which we have already met, is the principle of sufficient reason: every effect must have a cause. There must be some real observable difference that explains different outcomes.

Now we can see the problem. Considered in itself, the pair of triangles is just one thing. Each different relative orientation and time separation we give them depends on our whim. They should not have any effect. Yet each has momentous consequences: they create quite different universes. An exactly analogous problem arises if the universe consists of any number of particles. Two snapshots (the analogues of the two triangles) of the relative configuration of the universe are never quite enough to determine an entire history uniquely.

Before we look at the one possibility that can resolve this puzzle, it is worth considering how the four freedoms that do count show up in practice. We shall then be able to see what a great discovery Newton’s invisible framework was. We start with the twists.

When I was a boy, there was only one sport at which I was any good: the high jump. One year I went on a training course at the athletics ground in Oxford. We were introduced to angular momentum and how it could be exploited to improve the jump. As tallest of the young hopefuls, I was chosen to give a demonstration. The instructor made me lie on my side, arms and legs outstretched, on a small bench turntable. He started to rotate it slowly and asked, ‘If you pull yourself into a crouched position, what will happen?’ I knew, I was studying physics: ‘Angular momentum will be conserved, and the turntable will spin faster.’ ‘Right,’ he said, ‘do it.’ Proudly, I pulled in my arms and legs with vigour. The effect was frightening. The turntable whizzed around so fast that I panicked, tried to get off, and was thrown onto the floor. I escaped with bruises. I am still kicking myself, not about the accident, but because I did not stay on another day. I would have seen Roger Bannister run the first four-minute mile.

Angular momentum is a kind of net spin about a fixed axis. To calculate it for the Earth, you multiply the mass of each piece of matter in the Earth by its perpendicular distance from the rotation axis and the speed of its circular motion about the axis. The Earth’s total angular momentum is the sum of the contributions of all the pieces. Clockwise and anticlockwise motions count oppositely. A jet plane flying round the world in the opposite sense to the daily rotation contributes with the opposite sign.