Julian Barbour - The End of Time - The Next Revolution in Physics

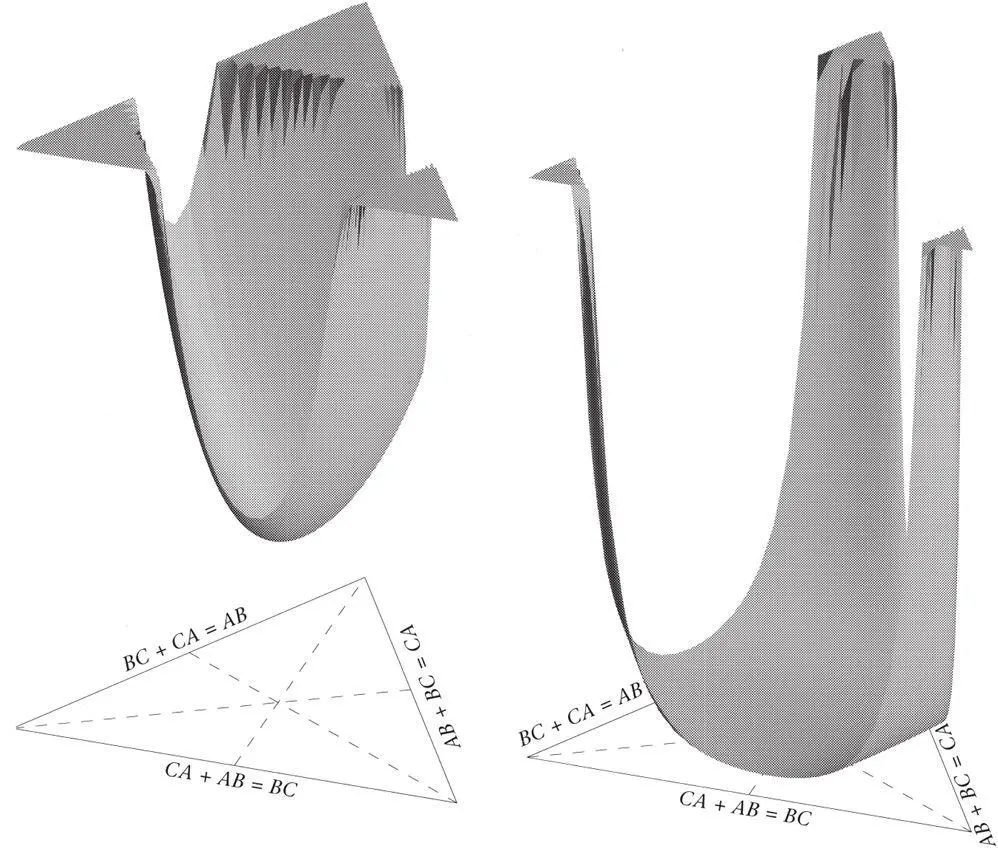
Figure 17.The gravitational potential energy of three bodies of different masses is shown as the height of a surface above Shape Space (Figure 8), each point on which corresponds to a different shape of the triangle formed by the three bodies. The overall scales of the configurations on the right are nine times greater, so the magnitude of the potential energy is much lower. Since potential energy is inversely proportional to separation, it increases sharply towards the corners of Shape Space, corresponding to two-particle coincidences, and becomes infinite at them. As this cannot be shown in the figure, the surfaces have been cut off at a certain height. The most distant corner of Shape Space corresponds in this figure to coincidence of the two most massive particles, so this is why the potential increases most strongly there.

Like angular momentum, the energy affects the appearance of systems and the behaviour of individual objects. For gravity the potential energy is negative, while the kinetic energy is positive. Thus the total energy E can be either positive, zero or negative. If a spacecraft is launched with sufficient speed, it can escape from the Earth’s gravity because its E is positive. If E is zero, the spacecraft has exactly the escape velocity, and escape is just possible. If E is negative, the spacecraft cannot escape from the Earth and will either orbit the Earth or fall back to ground. The planets can never escape from the Sun because they have negative E . Star clusters can remain concentrated in a relatively small region of space only if their energy is negative, otherwise they would rapidly disperse. This is why we do see such fine objects as the galaxies and star clusters in the sky. It is also largely the reason why the Sun and planets have their beautiful round shapes.

Thus, the shapes of almost all the objects astronomers observe in the sky reflect their energy and angular momentum. They, in turn, seem impossible to explain unless absolute space and time do exist and have a real influence, just as Newton claimed. The evidence for Newton’s invisible framework is written all over the sky. The evidence can be summarized as the two-snapshots problem . Suppose that snapshots of an isolated system taken at two closely spaced instants show only the separations of its bodies, not the overall orientations in absolute space. The separation in time between the snapshots is also unknown. If the system is a globular cluster, the snapshots contain millions of data. However, to determine the evolution of the system, four pieces of data are still lacking. They determine the kinetic energy (one piece of data) and the angular momentum (three pieces of data). Although they cannot be deduced from the two snapshots, they have a huge influence on the evolution, which can often be seen at a glance. A third snapshot will yield the data, but also much redundant information. The four missing pieces of data comprise the entire evidence for absolute space and time. Every system in the universe proclaims their existence. This seems to make nonsense of my claim that time does not exist. There appears to be more to the universe than its relative configurations. There is invisible structure, of which no trace can be found in Platonia.

The Aims of Machian Mechanics (1)(p. 71) In creating the beautiful diagrams that form such an important part of this section, Dierck Liebscher was able to draw on initial data devised by Douglas Heggie (University of Edinburgh), using software written by Piet Hut (Institute for Advanced Study), Steve McMillan (Drexel University) and Jun Makino (University of Tokyo). Dierck has written a very interesting book (alas, as yet published only in German) on the connection between different possible geometries and Einstein’s relativity theory (Liebscher 1999). It contains many striking computer-generated diagrams.

(2)Poincaré’s discussion is contained in his Science and Hypothesis , which, along with the writings of his contemporary, Mach, became a popular-science best-seller. In fact, in this book I am actually revisiting many of the themes discussed by Poincaré and Mach, but with the advantage of hindsight. How are the great issues they raised changed by the discovery of general relativity and quantum mechanics? I have adapted Poincaré’s discussion somewhat to match the requirements of a timeless theory (he considered only the possibility of eliminating absolute space).

(3)Since writing Box 3, which draws attention to the present unsatisfactory use of absolute dislance in physics, I have discovered a way to create dynamical theories in which distance is not absolute. This is achieved by a very natural extension of the best-matching idea described later in the book. The new insights that I mention in the Preface are in part connected with this development. One of the most exciting is that, if such theories do indeed describe the world, gravitation and the other forces of nature are precisely the mechanism by means of which absolute distance is made irrelevant. Since this work is still in progress, I shall make no attempt to describe it in detail, but I shall keep my website (www.julianbarbour.com) up to date with any progress (see also p.358).

Newton’s mysterious ‘timepiece’ and speeds measured relative to it figured prominently in the last chapter. But is it really there, and how can we ever read its time if it is invisible? This chapter is about these two questions.

A simple but famous experiment of Galileo provides strong evidence for something very like Newton’s absolute time. He rolled a ball across a table and off its edge. His analysis of its fall was a major step in mechanics. First he noted the ball’s innate tendency to carry on forward in the direction it had followed on the table. It also started to fall under gravity, picking up speed. Galileo conjectured that two processes were at work independently, and that each could be analysed separately. The total effect would be found by simply adding the two processes together.

Galileo’s recognition of the tendency to keep moving forward anticipated Newton’s law of inertia. He did not recognize it as a universal law, but he did make it precise in some special cases. For the example of the ball, he conjectured that but for gravity (and air resistance) the ball would move for ever forward with uniform speed. (He actually thought that the motion would be around the Earth – Galileo’s inertia was circular. Luckily, the difference was far too small to affect his analysis.)

As for the second process, Galileo had already found that if an object is dropped from rest and in the first unit of time falls one unit of distance, then in the next it will fall a further three, in the next five, and so on. He was entranced by this, and called it the odd numbers rule . Now consider the sequence:

at t = 1, distance fallen = 1,

at t = 2, distance fallen = 1 + 3 = 4,

at t = 3, distance fallen = 1 + 3 + 5 = 9,

at t = 4, distance fallen = 1 + 3 + 5 + 7 = 16,…

The distance fallen increases as the square of the time: 1 2= 1, 2 2= 4, 3 2= 9, 4 2= 16,... . Galileo’s originality was to seek for a deeper meaning in this pattern.

Many teenagers can now do in seconds a calculation that took Galileo a year or more – it was so novel. He asked: if the distance fallen increases as the square of the time, how does the speed increase with time? He eventually found that it must increase uniformly with time. If after the first unit of time the object has acquired a certain speed, then after the second it will have twice that speed, after the third three times, and so on. Galileo’s work showed that, in the absence of air resistance, a falling body always has a constant acceleration. It never ceases to amaze me what consequences flowed from Galileo’s simple but precise question. It taught his successors how to read the ‘great book of nature’ (Galileo’s expression). From a striking empirical pattern, he had found his way to a simpler and deeper law.