Julian Barbour - The End of Time - The Next Revolution in Physics

BOX 7 Tait’s Inertial Clock

Tait used the relativity principle (Box 5) to simplify things. If the particles are moving inertially, one can always suppose that particle 1 is at rest; it is shown in Figure 19 as the black diamond where the three coordinate axes x, y, z in absolute space meet. Now, unless the particles collide at some time – and we need not bother about this exceptional case – there must come a time at which particle 2 passes 1 at some least distance a . The coordinate axes can be chosen so that the line of its motion is as shown by the string of black diamonds. We can choose the unit of time so that particle 2 has unit speed. It will be Neumann’s clock, and each unit of distance it goes will mark one unit of time. Several positions of particle 2 are shown . They are the ‘ticks’ of the clock. At time t = 0, let particle 2 be at the point closest to particle 1 (at the black diamond on the x axis). At this time, particle 3 can be anywhere (three unknown coordinates) and have any velocity (three more unknowns). Thus, seven numbers are unknown: six for particle 3 and the distance a .

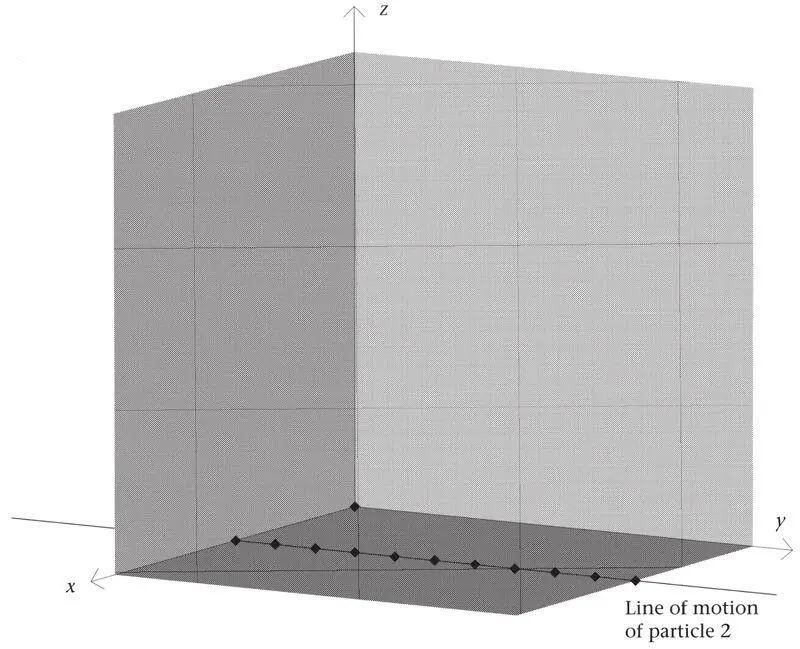
Figure 19.The arrangement of coordinates in Tait’s problem.

Now, each snapshot contains three independent data – the three sides of the triangle at the instant of the snapshot. It would seem that three snapshots give nine data – more than enough for the accomplished Tait to solve the problem. But since we know none of the times at which the snapshots are taken, each gives only two useful data. Thus, four snapshots will give eight useful data, seven of which will establish the Newtonian frame into which the triangles fit, while the remaining one will verify that they are indeed obeying Newton’s law. Figure 20 shows a typical solution.

Figure 20.A solution of Tait’s problem. The four ‘snapshots’ of the triangles (the given data) are shown in plan, with an indication of their positions in the ‘sculpture’ of four triangles created by the solution.

Tait’s solution creates nothing less than Newton’s invisible framework. It is both absolute space and the positions of the triangles in it at different instants of ‘time’. We start with triangles. They are all that we have. We are told that they are not random triangles but have arisen through a law. We test this assertion and succeed in creating a simple ‘sculpture’ of three straight lines. The order created is dramatic. Apart from exceptional cases, the distances of the particles from one another do not change in a mutually uniform manner. In fact, they vary with respect to one another in a quite complicated way. Moreover, the triangles in themselves give no hint that there is any space in which their corners lie on straight lines. Yet such lines can be found.

It is equally remarkable that the motions along these lines are mutually uniform. Each particle is the ‘hand’ of a clock for the motion of the other two. The sculpture is a clock with many hands (two in this case, since particle 1 defines the origin). And, now that we have the rigid structure, we see that absolute space is redundant. The sculpture holds together on its own. The ‘room’ was never there until it was created from the triangles and rules. It is they that give an almost bodily tangibility to space and time.

They also explain the meaning of duration and the statement that a second today is the same as a second tomorrow. Duration is reduced to distance. If today or tomorrow any one of the ‘hands’ of the inertial clock moves through the same distance, then we can say that the ‘same amount of time’ has passed. The extra time dimension is redundant: everything we need to know about time can be read off from distances. But note how special is the distance that leads to a meaningful definition of duration. Any change of distance ‘labels’ the instants of time. In statements like ‘Particle A hits B when C is five metres from D ’, ‘five metres’ identifies an instant of time – it labels the instant. That is sufficient for history. However, the obvious changes of distance – those between particles – do not lead to a sensible definition of duration. The secrets of time are rather well hidden.

A similar construction can be repeated for any number of particles – a hundred, a billion, quite enough to fill the sky and make a galaxy or even a universe. It is important that if there are more than five particles then three snapshots are already sufficient to solve Tait’s problem, but two are never enough. This is very odd. For a thousand bodies, three snapshots contain far more information than we need, but two never give quite enough. The problem is exactly the one we encountered earlier. Two snapshots tell nothing about the relative orientations or the separation in time. We lack four pieces of information, and all the mystery of absolute space and time resides in them. We cannot make a clock until we get our hands on them. But when we have them, the properties that are revealed are very striking.

For example, Tait’s construction is a good model for the motions of many thousands of stars that are relatively close neighbours of our Sun. They all ‘fall’ in the gravitational field of the Galaxy in much the same way. That motion hardly shows up in the relative separations. But also, because the stars are so far apart there is very little gravitational interaction between them. Their motions are thus well described by the construction. What is more, any three stars can be chosen to make a ‘Tait clock’ and tell the time. Any other three will make another. Thousands, millions of such clocks can be made. All these clocks, light years apart, keep time with one another.

I mentioned earlier the importance of not being misled by the special circumstances of our existence. One of them is the Earth. Only the tiniest fraction of the matter in the universe is in solid form. Indeed, only a small fraction of the Earth – its crust, on which we live, and the innermost core – is solid. This is our home, and we take it for the normal run of things. The ground, trees, buildings, hills and mountains make a framework, which is so like absolute space. It does seem quite natural that a body should move in a straight line in such a space. But we need to think what the universe in its totality is like. Take a billion particles and let them swarm in confusion – that is the reality of ‘home’ almost everywhere in the universe. The stars do seem to swarm, so do the atoms in the stars. To understand the real issues of timekeeping, we must imagine trying to do it in typical circumstances. We must master celestial timekeeping and not be content with the short cuts that can be taken on the Earth, for they hide the essence of the problem.

We have seen how to check whether bodies are moving inertially without prior access to absolute space and time. But all matter in the universe interacts. Interactions make things more complicated, and not only because the calculations are hard. If objects are moving inertially, any three will suffice to construct an inertial clock. But in a system of interacting bodies it is not possible to treat any of them separately because each is affected by the others. In addition, we can find no framework at all in which the bodies move uniformly in straight lines.

There are three parts to a clock: a mechanism, a clock-face and hands. The main problem of celestial timekeeping arises because the clock-face is invisible. A further problem is that the hands run at varying rates. Imagine an isolated system of three gravitationally interacting stars. We are again given only their relative positions, from which we are to construct a clock. Because of their interactions, no framework exists in which the three stars move along straight lines. The best we can achieve is some ‘spaghetti sculpture’ (Figure 13). This is found by telling a computer that there does exist a framework of absolute space and time in which the stars obey Newton’s laws. However, the computer is given only the successive relative positions, not the positions in the framework at given times. But this is real information, and if the computer is given a sufficient number of snapshots it can search for an arrangement of them in a spaghetti sculpture in which the stars do obey Newton’s laws. The positions in the framework and the separations in time are found by trial and error.