Julian Barbour - The End of Time - The Next Revolution in Physics

To analyse the falling ball, Galileo simply combined the two processes – inertia and falling – under the assumption that each acts independently. He obtained the famous parabolic motion (Figure 18). In each unit of time, the ball moves through the same horizontal distance, but in the vertical dimension the distance fallen grows as the square of the time. The resulting curve traced by the ball is part of a parabola. Newton applied Galileo’s method for terrestrial motions to the heavens, and showed that the laws of motion had universal validity. This was the first great unification in physics. There may be a lesson for us here in our present quest – the search for time. We may have to look for it in the sky.

A search is needed. It is striking that all the elements in Galileo’s analysis are readily visualized. You can easily call up a table and the parabola traced by the ball in your imagination. Yet one key player seems reluctant to appear on the stage. Where is time? This is the question I have so far dodged. It presents a severe challenge to the idea that configurations are all that exist. Suppose that we take snapshots of the ball as it rolls across Galileo’s table in Padua, where he experimented. These snapshots can show everything in his studio. However, only the ball is moving. We take lots of snapshots, at random time intervals, until the ball is just about to fall over the edge. We put the snapshots, all mixed up, in a bag and, supposing time travel is possible, present it to Galileo and ask him whether, by examining the snapshots, he can tell where the ball will land.

He cannot. Had we rolled the ball twice as fast, it would have passed through the identical sequence of positions to the table’s edge, and they are all the snapshots capture. The speed is not recorded. But the ball’s speed determines the shape of the parabola, and hence where the ball lands. In fact Galileo will not even know in which direction the ball is going. Perhaps it will fall off the right-hand side of the table. More clearly than with the three-body evolutions, which mix the effects of time and spin, we see here the entire evidence for absolute time. The speed determines the shape of the parabola. There is manifestly more to the world than the snapshots reveal. What and where is it? Galileo himself provides an answer of sorts. He tells us that he measured time by a water-clock – a large water tank with a small hole in the bottom. His assistant would remove a finger from the hole and let the water flow into a measuring flask until the timed interval ended. The amount of water measured the time.

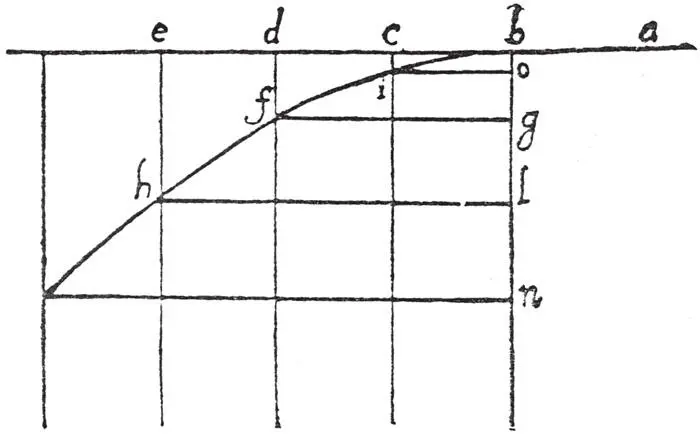
Figure 18.Galileo’s own diagram of parabolic motion. The ball comes from the right and then starts to fall. Incidentally, this diagram illustrates how conventions get established and become rigid – a modern version of it would certainly show the ball coming from the left and falling off on the right.) The uniformity of the horizontal inertial motion is shown by the equality of the intervals be, cd, de, ..., while the odd-numbers rule is reflected in the increasing vertical descents bo, og, gl, ....

We have only to include the water tank and assistant in the snapshots, and everything is changed. Galileo can tell us where the ball will land because he can now deduce its speed. There are some important lessons we can learn from this. First, it is water, not time, that flows. Speed is not distance divided by time but distance divided by some real change elsewhere in the world. What we call time will never be understood unless this fact is grasped. Second, we must ask what change is allowed as a measure of time. Galileo measured the water carefully and made sure that it escaped steadily from the tank – otherwise his measure of time would surely have been useless. But the innocent word ‘steadily’ itself presupposes a measure of time. Where does that come from? It looks as if we can get into an unending search all too easily. No sooner do we present some measure that is supposed to be uniform than we are challenged to prove that it is uniform.

It is an indication of how slowly basic issues are resolved – and how easily they are put aside – that Newton highlighted the issue of the ultimate source of time nearly two hundred years before serious attempts were made to find it. Even then, the attempts remained rather rudimentary and few scientists became aware of them. It is interesting that Galileo had already anticipated the first useful attempt. This was actually forced upon him by the brevity of free fall in the ball experiment: it was all over much too quickly for the water-clock to be of any use. (It came into its own when Galileo rolled balls down very gentle inclines.) To analyse the parabola, he found a handy substitute. He noted that if the horizontal motion of the falling ball does persist unchanged, then the horizontal distance traversed becomes a direct measure of time. He therefore used the horizontal motion as a clock to time the vertical motion. His famous law of free fall was then coded in the shape of the parabola. Its defining property is that the distance down from the apex (where the ball falls off the table) increases as the square of the horizontal distance from the axis. But this measures time.

Thus, time is hidden in the picture. The horizontal distance measures time. It would be nice if one could say ‘the horizontal distance is time’. This is the goal I am working towards: time will become a distance through which things have moved. Then we shall truly see time as it flows, because time will be seen for what it is – the change of things. However, there are many different motions in the universe. Are they all equally suitable for measuring time? A second question is this: what causal connections are at work here? Galileo measured time by the flow of water, but it is hard to believe that a little water flowing out of a tank in the corner of his studio directly caused the balls to trace those beautiful parabolas through the air. If time derives from motion and change – and it is quite certain that all time measures do – what motion or change, in the last resort, is telling the ball which parabola to trace? The first question is more readily answered.

Nearly two thousand years ago, astronomers knew that some motions are better than others as measures of time. This they discovered experimentally. For the early astronomers, there were two obvious and, on the face of it, equally good candidates for telling time. Both were up in the sky and both had impressive credentials. The stars made the first clock, the Sun the second.

The stars remain fixed relative to each other and define sidereal time . Any star can be chosen as the ‘hand’ of the stellar clock: one merely has to note when it is due south. The stellar clock then ticks whenever that star is due south (i.e. when it crosses the meridian). Fractions of the ‘tick unit’ are measured by its distance from the meridian. A mere glance at the night sky could tell the ancient astronomers the time to within a quarter of an hour. With some care, times could be told to a minute. There is something wonderful about this great clock in the sky. It was a unique gift to the astronomers. The discoveries that culminated with Kepler’s laws of planetary motion, and many more made until well into the twentieth century, are unthinkable without it. No other phenomenon in nature could match it for convenience and accuracy. In millennia it has lost a few hours.

But there is a rival – the Sun. It defines solar time . This is the clock by which humanity and all other animals have always lived. The principle is the same: it is noon when the sun crosses the meridian. You don’t even have to be an astronomer to tell the time by this clock; a sundial will do.