Julian Barbour - The End of Time - The Next Revolution in Physics

In fact, if the work with Niall O Murchadha mentioned at the end of the Preface, which suggests that absolute distance can be eliminated as a basic concept (see Box 3), can be transformed into a complete theory, the problem of infinity may well be solved in the process. If size has no meaning, the distinction between a spatially finite or infinite universe becomes meaningless.

Merely changing the framework in which one conceives of the universe does nothing, but it is still very illuminating to look at some fundamental facts of mechanics in the alternative arenas of absolute space and Platonia. This exercise brings out the strengths of Newton’s position, and at the same time shows what a Machian approach must achieve. The following discussion is based on penetrating remarks made in 1902 by the great French mathematician Henri Poincaré. More clearly than Mach, he demonstrated what is required of a theory of relative motion. Unfortunately, his remarks were overshadowed by Einstein’s discovery of relativity and did not attract the attention they deserved – and still deserve.

You may find that this chapter requires more reflection than all the others. You certainly do not need to grasp it all, but I hope that you will be able to change from a way of thinking to which we have been conditioned by the fact that we evolved on the stable surface of the Earth to a more abstract way of thinking that would have been forced upon us had we evolved from creatures that roamed in space between objects moving through it in all directions. We have to learn how to find our bearings when the solid reassuring framework of the Earth is not there. This is the kind of mental preparation you need to understand the ideas Poincaré developed. In this respect, he was smarter than Einstein.

Poincaré simply asked, rather more precisely than anyone before him, what information is needed to predict the future. Another French mathematician, Pierre Laplace, had already imagined a divine intelligence that at one instant knows the positions and motions of all bodies in the universe. Using Newton’s laws, the divinity can then calculate all past and future motions – it can see, in its mind’s eye, all of history laid out for the minutest inspection. As an alternative to the standard representation in Newton’s absolute space, it will help to see this miracle performed in Triangle Land, the simplest Platonia. This will reveal a curious defect in Newtonian mechanics.

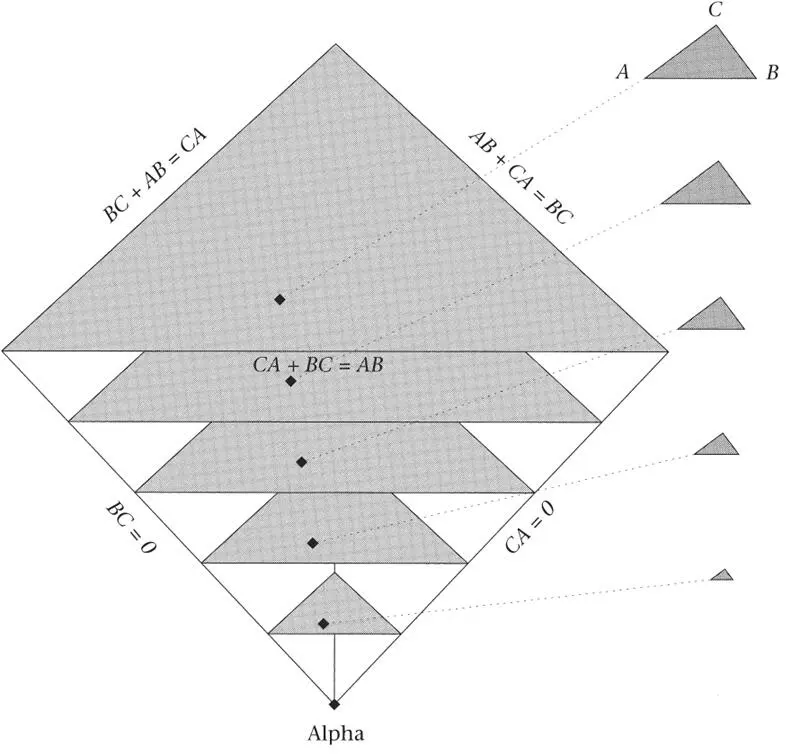
Figure 7.Here Alpha, the apex of Triangle Land, is at the bottom. The axes that were shown in Figures 3 and 4 have been removed since they would detract from the essence of this and the following figure. Two of the ribs of Triangle Land run upwards to the right and left. They are marked BC = 0 and CA = 0 to indicate that the triangles corresponding to points on these ribs have ‘collapsed’ because their sides BC and CA, respectively, are zero. The third rib recedes into the figure (this is the rib that in Figure 4 runs along the ‘floor’). The shaded planes cut the faces of the pyramid in the lines on the ‘sheets’ in Figure 4. As shown here, all points on any straight line from Alpha through Triangle Land represent different triangles, but they differ only in size. In fact, all the points on any one of the shaded sheets represent triangles that have the same perimeter. If we are interested only in the shapes of the triangles, these are represented by the points on just one of the planes (i.e. the different points on any one plane represent differently shaped triangles; this possibility is depicted more fully in Figure 8).

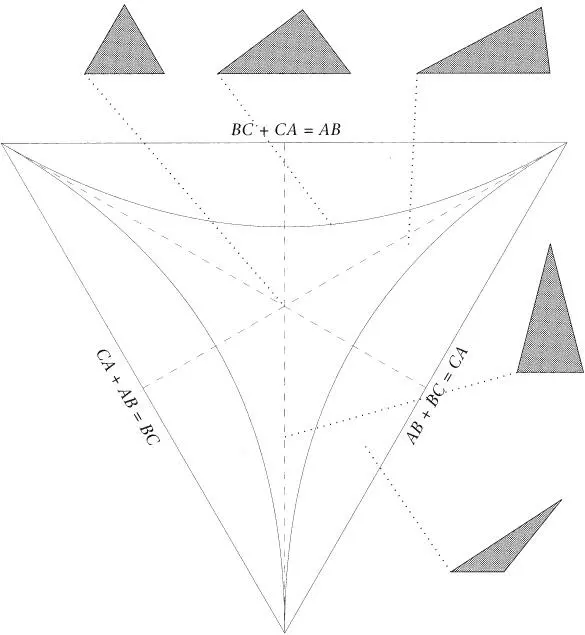
Figure 8.This shows one of the shaded planes in Figure 7. It can be called Shape Space, because each point in it represents a different possible shape of a triangle. The point at the centre represents an equilateral triangle (all three sides equal). Points on the three dashed lines correspond to isosceles triangle (two sides equal). All other possible triangles are scalene (all three sides unequal). Points on the three curved lines correspond to right-angled triangles (the central triangle at the top is the Pythagorean 3, 4, 5 triangle). All points inside the curved lines correspond to acute triangles (all angles less than 90°); all points outside the curved lines correspond to obtuse triangles (one angle greater than 90°). When I asked my friend Dierck Liebscher to create this diagram, I had no idea that it would turn out to be so beautiful. I do like the curved lines of the right-angled triangles! Let me remind you that all the points on the straight edges of Shape Space correspond to triangles that have become ‘flat’ because all three corners of each of these triangles are collinear (on one line). Each of the three vertices of Shape Space correspond to configurations in which two particles coincide, while the third is some distance from them.

You may like to refresh your memory by returning to Figures 3 and 4 before you examine Figures 7 and 8. Figures 3, 4, 7, 8 and 9 are very important. I am rather concerned that younger readers (those under forty, or even fifty!) may have some difficulty with them, since fundamental geometry is not taught nearly as thoroughly at school as it used to be. However, if you can spend a bit of time on these figures and begin to understand what they mean, you will certainly get a great deal more out of this book. In fact, you will also be absorbing some of the deepest and most fruitful concepts in mathematics and theoretical physics. Don’t worry – it can be done. Once the clutter of technical detail is removed, all the great ideas in mathematics and physics are in essence very simple and intuitive. But you need patience to absorb them. When Newton was asked how he had come to make his great discoveries, he answered: ‘By thinking about these things for a long time.’ Try lying in bed or a nice warm bath and thinking about Triangle Land!

Figure 8 brings out the rich topography of any Platonia (Shape Space is a possible Platonia). Wherever you go, you find something different. Each point is a different ‘world’ – and a different instant of time. There are even characteristically different regions (of acute and obtuse triangles), like provinces or counties, as well as internal and external frontiers (the right-angled and isosceles triangles). Any Platonia is quite unlike Newton’s absolute space, all points of which are identical. As I remark in the Notes to Chapter 4, there is something unreal about that property of absolute space. Real things have genuine attributes that distinguish them from other real things. Platonia is a land of real things. I find Figure 8 very suggestive. Leibniz always said that it is necessary to consider all possible worlds and find some reason why one rather than another occurs or is actually created. In Figure 8, we do see all the possible worlds of triangle shapes laid out before us. Box 3 contains a short digression on possible kinds of Platonias.

BOX 3 Possible Platonias

One of the big unsolved problems of physics is the origin of distance and whether it is absolute. Since we need a measuring rod to measure any distance, this suggests rather strongly that distance is relative (to the chosen rod). If we tried to double every distance in the universe, the length of the rod would be doubled too, and nothing actually observable would be changed. For reasons like this, physicists have a hunch that absolute scale should have no objective meaning. However, this is not confirmed by existing theories and experimental facts, which do suggest that distance is in a well-defined sense absolute. The hope remains that a physics completely without scale will be found. If so, Shape Space gives an idea of what the corresponding Platonia will be like. There is still a uniquely distinguished point in it – the central point in Figure 8. It takes the place of Alpha in Triangle Land. If you ‘touched’ the central point, the equilateral triangle would ‘light up’. This is the most symmetrical configuration the three-body universe can have. Symmetry is beautiful in one way but bland in another. The boundaries of Shape Space are somewhat unappealing too, because they represent improper triangles that flatten into a line (mathematicians call such configurations, collinear in this case, degenerate). The vertices of Shape Space correspond to collinear configurations in which one particle is infinitely far from the other two. The interesting structures in this case lie between the bland centre and the degeneracy of the frontiers.