Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Взвешенные в жидкости мельчайшие частицы находятся в беспорядочном движении, которое называется броуновским. Это явление было обнаружено шотландским ботаником Робертом Броуном в 1827 году. Наблюдая под микроскопом за поведением зерен пыльцы, он заметил, что эти мелкие частицы (около одного или двух микрометров в диаметре) двигаются в жидкости случайным образом (см. илл.).

Их хаотичное движение объясняется ударами, испытываемыми частицами со стороны молекул жидкости. Броуновское движение – своего рода обращение, направленное молекулами человеку XIX века: «Вы нас не видите, но мы здесь!» Это сообщение было расшифровано французскими физиками, в частности Луи Жоржем Гуи (1854–1926), лишь в конце XIX века. К тому времени уже стало известно, что молекулы при повышении температуры движутся быстрее. Фактически температура является мерой кинетической энергии молекул. В броуновском движении часть этой кинетической энергии передается мелким частицам, что и приводит к их движению, которое впервые и обнаружил Роберт Броун.

Погруженная в жидкость частица движется хаотично

Рассмотрим атом самого простого элемента, водорода, который состоит из протона и электрона. Первое по существу верное описание атома водорода привел британский физик Эрнест Резерфорд (1871–1937). Он выяснил, что электрон, обладающий отрицательным зарядом – e , и протон, несущий заряд такой же по величине, но противоположный по знаку, удерживаются вместе благодаря электростатическому взаимодействию. При этом электрон вращается вокруг протона подобно тому, как Земля вращается вокруг Солнца. Заметим, что в таком описании вращающийся электрон представляет собой циркулярный электрический ток. Однако любой замкнутый контур, по которому проходит ток, подобно антенне испускает электромагнитное излучение. В результате, согласно описанию Резерфорда, электрон должен был бы терять энергию… и в конечном итоге «упасть» на протон (илл. 3)! Но мы знаем, что он не падает – атом водорода стабилен. Чтобы дать объяснение этому факту, необходимо было ввести некий новый физический принцип, который выходил бы за рамки ньютоновской физики. Им стал принцип неопределенности Гейзенберга.

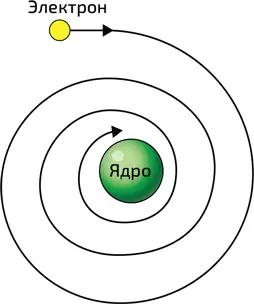
3. В классической физике атом Резерфорда был бы нестабилен: электрон в конце концов упал бы на ядро

В соответствии с этим принципом бедный электрон должен вращаться в области пространства некоторого размера с плохо определенной, но не равной нулю скоростью. И из этих смутных соображений мы собираемся оценить размер атома!

Пусть v и 2 R суть скорость электрона и диаметр сферы, в пределах которой он движется. Согласно формуле (1), 2 mRv > ħ . Следовательно, кинетическая энергия электрона, равная mv 2/2, не может быть меньше чем ħ 2/(8 mR 2). Добавляя электростатическую энергию его взаимодействия с протоном, находим неравенство для полной энергии электрона W :

где элементарный заряд e равен 1,6∙10 –19Кл, а ε o – диэлектрическая проницаемость вакуума, константа, равная 8,85∙10 –12Ф∙м –1.

Энергия W атома не может стать ниже минимума этого выражения, который, как легко понять, реализуется при R = R 0 , где

Равновесное состояние механической системы соответствует минимуму ее потенциальной энергии (см. главу 11, «Струны и резонатор»). Радиус атома R не может сильно превышать величину R 0 , потому что потенциальная энергия электрона при этом была бы слишком высока; но он не может быть и намного меньше R 0 , потому что тогда кинетическая энергия была бы слишком велика, а полная энергия должна сохраняться. Именно поэтому электрон и не падает на ядро! Выражение (3) дает нам представление о размере атома водорода – это примерно 1 ангстрем (десятая часть нанометра).

Пребывая в своем основном состоянии (минимума полной энергии), атом терять энергию не может. Однако он может ее получать, переходя при этом в то или иное «возбужденное» состояние. При этом бесконечно долго возбужденным он не остается – через некоторое время, излучая свет, атом возвращается в свое основное состояние. Этот свет соответствует излучению точно определенных частот, то есть спектр излучения атома является «линейчатым» (см. главу 7, «От спектров атомов до спектра абсолютно черного тела»). Частоты спектральных линий образуют так называемое дискретное множество, то есть их можно пронумеровать, например, в зависимости от интенсивности каждой из них. Чтобы объяснить происхождение такого линейчатого спектра, разумно предположить, что значения, которые может принимать энергия данного атома, также составляют дискретное множество. Поскольку свет может излучаться только в виде фотонов (см. главу 7, «От спектров атомов до спектра абсолютно черного тела»), то закон сохранения энергии требует, чтобы энергия hυ каждого фотона была равна разности между двумя допустимыми значениями энергии атома (илл. 4). Таким образом, дискретный вид спектра излучения объясняется, по крайней мере, качественно. Остается выяснить, почему значения энергии атома составляют дискретное множество.