С помощью уравнения Шрёдингера оказалось возможным найти пространственное распределение плотности вероятности электрона для его возможных состояний в атоме водорода. Изобразив эти распределения плотности вероятности на плоскости разными цветами, получают изображение различных атомных орбиталей (областей, в которых вероятность нахождения электрона наиболее высока). Такие изображения заменяют электронные орбиты модели атома Бора (илл. 5) и наглядно представляют поведение электронов в атоме. Основанные на уравнении Шрёдингера расчеты объясняют существование дискретных уровней энергии, которые и являются причиной линейчатых спектров, наблюдаемых при излучении и поглощении света. Подобные, но более сложные вычисления позволяют понять, как между атомами образуются химические связи.
Заметим, что работы де Бройля и Шрёдингера предшествовали открытию Гейзенбергом принципа неопределенности. Последний прост, краток, элегантен, однако содержит меньше информации, чем уравнение Шрёдингера.
Опыт Дэвиссона – Джермера
Предложенная де Бройлем концепция связи между волнами и частицами, так называемый корпускулярно-волновой дуализм, привела к идее применения оптических методов исследования с заменой света на потоки частиц. Так, в 1927 году американские физики Клинтон Дэвиссон и Лестер Джермер бомбардировали электронами кристалл никеля. В результате они получили дифрактограммы, подобные возникающим при облучении кристаллов рентгеновскими лучами (см. врезку). Для интерпретации полученных дифракционных картин электронам следовало приписать определенную длину волны, и она совпадала с величиной, предсказанной де Бройлем. Таким образом, эксперимент блестяще подтвердил его гипотезу.
Принцип неопределенности позволяет получить интересную информацию о движении атомов в твердых телах. Под твердыми телами здесь мы будем подразумевать кристаллы (см. главу 9), поскольку при низких температурах кристаллическая структура является устойчивой формой существования почти всех чистых веществ. Атомы в кристалле не являются неподвижными: они колеблются вокруг положения равновесия. Амплитуда этих колебаний очень мала: расстояние между двумя соседними атомами всегда остается близким к своему среднему значению, которое составляет около нескольких десятых нанометра. Как правило, эти колебания обусловлены тепловым движением: чем температура выше, тем больше амплитуда колебаний (см. главу 22, врезку «Броуновское движение»). Что же происходит, когда температура опускается до абсолютного нуля (0 К, то есть –273,15 °C)? Можно предположить, что колебания прекращаются и атомы замирают. Однако в этом случае их положение было бы точно фиксировано, в то время как скорость была бы равна нулю, то есть Δ x = Δ p = 0, что нарушило бы соотношение неопределенности (1) (см. главу 22). Отсюда следует, что движение атомов прекратиться не может даже при абсолютном нуле температур: в этом случае тепловые колебания сменяются на «нулевые колебания».
Попробуем разобраться в этом подробнее на примере простого кристалла, состоящего из атомов лишь одного сорта (например, водорода, кислорода, железа). Упрощенное, но качественно приемлемое описание движения атома в кристалле относительно его соседей можно получить, предполагая, что при отклонении от положения равновесия на него действует возвращающая сила, пропорциональная расстоянию, так как если бы его удерживала пружина. В таком случае движение атома относительно положения равновесия описывается формулой x ( t ) = x 0 cos (ω t – α), где x 0 – максимальная амплитуда колебаний (для двух других координат формулы аналогичны). При этом скорость атома v x ( t ) = –ω x 0 sin (ω t – α). Соотношение неопределенности требует, чтобы Δ x Δ v ≥ ħ / m , и, следовательно, ω x 0 2было не менее ħ / m , где m – масса атома. Частота ω для большинства веществ лежит в диапазоне между 10 13и 10 14Гц (характерную частоту колебаний атома в твердых телах называют частотой Дебая). Заменяя массу m на A m n , где A – массовое число (см. главу 13, врезку «Элементы ядерной физики»), а m n – средняя масса нуклона (около 1,67⋅10 –27кг), получим, что x 0 в метрах должна составлять не менее 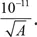 Это условие устанавливает верхнюю границу для амплитуды нулевых колебаний в 1/100 нм, которая, как правило, мала в сравнении с равновесным расстоянием между соседними атомами. Поэтому нет оснований полагать, что нулевые колебания в твердых телах разрушают его устойчивость.
Это условие устанавливает верхнюю границу для амплитуды нулевых колебаний в 1/100 нм, которая, как правило, мала в сравнении с равновесным расстоянием между соседними атомами. Поэтому нет оснований полагать, что нулевые колебания в твердых телах разрушают его устойчивость.
Читать дальше
Конец ознакомительного отрывка
Купить книгу

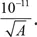 Это условие устанавливает верхнюю границу для амплитуды нулевых колебаний в 1/100 нм, которая, как правило, мала в сравнении с равновесным расстоянием между соседними атомами. Поэтому нет оснований полагать, что нулевые колебания в твердых телах разрушают его устойчивость.
Это условие устанавливает верхнюю границу для амплитуды нулевых колебаний в 1/100 нм, которая, как правило, мала в сравнении с равновесным расстоянием между соседними атомами. Поэтому нет оснований полагать, что нулевые колебания в твердых телах разрушают его устойчивость.


![Лина Сайфер - Театр мыльных пузырей [litres]](/books/434478/lina-sajfer-teatr-mylnyh-puzyrej-litres-thumb.webp)






