Андрей Варламов - Физика повседневности. От мыльных пузырей до квантовых технологий

Сомнения могут оставаться только для наименьших значений A , то есть для водорода ( A = 1) и гелия ( A = 4). Оказывается, что только гелий (He) является исключением из правила: если давление не превышает 2,5 Мпа, то нулевые колебания действительно делают его кристаллическое состояние неустойчивым при любых температурах. Все остальные простые тела, включая водород H 2 , при приближении температуры к абсолютному нулю рано или поздно затвердевают при любом давлении.

Мы уже видели, что согласно квантовой механике ни в какой момент времени невозможно установить точные значения положения r →и скорости v →электрона, вращающегося вокруг ядра. Еще более необычными оказываются свойства его магнитного момента.

Магнитный момент – это векторная величина, характеризующая свойство определенных объектов ориентироваться в магнитном поле. Например, стрелка компаса располагается по магнитному полю Земли, указывая направление на Северный магнитный полюс. Многие из элементарных частиц и объектов атомного масштаба также обладают магнитным моментом: электрон, нейтрон, протон, а также бо́льшая часть ядер, атомов и ионов.

Пространственные составляющие магнитного момента обозначаются как µ x , µ y , µ z . Когда стрелка компаса сориентирована в определенном направлении, то четко определены и все три составляющие ее магнитного момента. В отличие от компаса, электрон или нейтрон являются объектами, принадлежащими к квантовому миру. Для них может быть измерена только одна из трех составляющих магнитного момента, при этом она способна принимать только два противоположных значения: –µ или +µ. Это, казалось бы, парадоксальное утверждение было подтверждено экспериментально: первыми опытные данные, говорящие в пользу квантования магнитного момента представителей квантового мира, еще в 1922 году получили Отто Штерн и Вальтер Герлах. В своих экспериментах они направляли пучок атомов серебра (которые благодаря электронам внешней оболочки обладают магнитным моментом) сквозь неоднородное магнитное поле. В результате было обнаружено, что этот пучок разделяется строго пополам, что и доказывает квантование магнитного момента всего на два дискретных значения (илл. 8). Действительно, если бы магнитный момент мог принимать хотя бы три значения, то и пучок делился бы натрое, а если бы магнитный момент атомов серебра мог меняться непрерывно, то и пучок просто расходился бы в конус.

Еще несколько слов о пучке атомов серебра. Выберем ось x вдоль направления магнитного поля. Тогда существует такое состояние атома серебра, в котором µ x = –µ, и другое, в котором µ x = +µ. Существует также состояние, при котором µ y = µ. Что произойдет, если частица находится в этом состоянии и измеряется компонент µ x ? Измерение с равной вероятностью даст µ x = –µ или µ x = +µ. Таким образом, среднее значение всех измерений µ x , которые можно произвести в состоянии µ y = µ, равно нулю. То же самое относится к среднему значению всех измерений µ x в состоянии µ y = –µ. Чтобы принять в расчет эти свойства, в квантовой механике считается, что состояние µ y = µ является «соединением» состояний µ x = –µ и µ x = µ.

Если частица находится в состоянии с µ x = µ, магнитный момент получится ±µ с той же вероятностью, и поэтому среднее значение большого числа мер будет равно нулю. Это то же самое из средних измерений, которые можно выполнить с магнитным моментом в состоянии µ x = –µ. Чтобы понять значение этого свойства в рамках квантовой механики, утверждается, что состояние µ y = µ на самом деле представляет собой смесь состояний, имеющих µ x = + µ и µ x = –µ.

Результат, предсказываемый классической физикой: непрерывная линия.

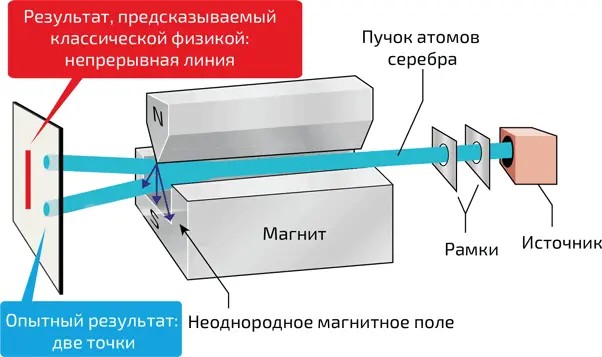
8. Принцип опыта Штерна – Герлаха. Атомы серебра проходят через вертикально направленное неоднородное магнитное поле. Согласно классической физике, пучок частиц с непрерывным распределением магнитного момента должен расходиться конусом. Опыт же показывает, что он делится на две компоненты