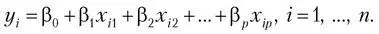Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]

3. Если функция потерь изменилась существенно и мы не достигли максимального числа повторений расчета, то пересчитаем коэффициенты, исходя из градиента, и идем к шагу 2.

4. Считаем, что оптимизация завершена, возвращаем модель с вычисленными коэффициентами.

Графически градиентный спуск выглядит как на рис. 8.4.

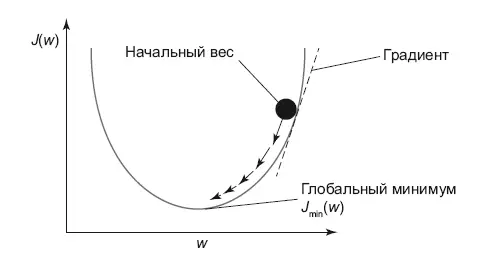
Рис. 8.4.Градиентный спуск

У нас есть функция потерь, и с произвольной точки мы двигаемся в сторону ее минимума последовательно, по шагам.

У этого алгоритма есть еще две версии: стохастический градиентный спуск (SGD) и пакетный (Mini Batch Gradient Descent). Первый используется для работы с большими данными, когда мы из всего датасета используем только один пример для одной итерации обучения. Альтернативной для больших данных является пакетная версия (batch) этого алгоритма, которая вместо одного примера использует подмножество датасета.

Самая простая и популярная модель регрессии. На самом деле ее мы затрагивали в школе, когда писали формулу линейной зависимости. Когда я учился в старших классах, она выглядела так: y = k × x + b . Это так называемая простая линейная регрессия, в ней всего одна независимая переменная.

Обычно работают с множественной линейной регрессией (multivariate linear regression), формула которой выглядит так:

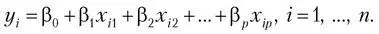
Она состоит из суммы произведений коэффициентов на значение соответствующей фичи и дополнительно свободного члена (intercept). Выглядит она как прямая в случае одной независимой переменной и как гиперплоскость в случае N фич. Когда происходит обучение линейной регрессии, то гиперплоскость строится таким образом, чтобы минимизировать расстояние от точек (из датасета) до нее, что является среднеквадратичным отклонением. Самый первый вопрос, который я задаю кандидатам на должность аналитика данных, звучит так: «У вас есть результат эксперимента, точки отмечены на плоскости с двумя осями. Кто-то провел линию, их аппроксимирующую. Как понять, оптимально ли построена прямая?» Это очень хороший вопрос на понимание сути линейной регрессии.

Если данные на входе линейной регрессии были нормализованы, то чем больше коэффициент у фичи, тем большее влияние на зависимую переменную она оказывает, а значит, и на результат. Положительный коэффициент – увеличение значения фичи увеличивает значение зависимой переменной (положительная корреляция). Отрицательная – это отрицательная корреляция или отрицательная линейная зависимость.

Это самая популярная модель решения задач бинарной (два класса) классификации.

Допустим, у нас есть задача – разделить два класса: крестики и нолики. Я их отметил на координатной сетке, по осям отложил значения фич X1 и X2 (рис. 8.5). Легко видеть, что между крестиками и ноликами можно провести прямую, которая их разделяет. Все, что выше прямой, – нолики, ниже – крестики.

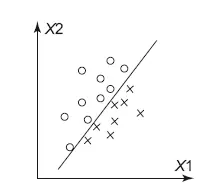
Рис. 8.5.Разделяющая прямая в задаче классификации

Так работает логистическая регрессия – она ищет прямую или гиперплоскость, которая разделяет классы с минимальной ошибкой. Как результат она выдает вероятность принадлежности точки к классу. Чем ближе точка находится к разделяющей поверхности, тем менее модель уверена в своем выборе, вероятность будет приближаться к 0.5, чем дальше точка от поверхности – тем вероятность ближе к 0 или 1, в зависимости от класса. В задаче два класса, поэтому если вероятность принадлежности к одному классу равна 0.3, то ко второму 1–0.3 = 0.7. Для вычисления вероятности в логистической регрессии используется сигмоида (рис. 8.6).

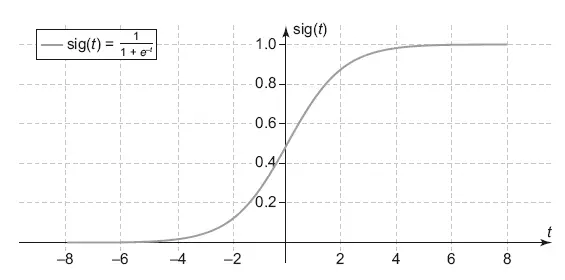
Рис. 8.6.Сигмоида

В этом графике в t подставляется значение из обычной линейной формулы с коэффициентами, как у линейной регрессии. Сама формула является уравнением той разделяющей поверхности, о которой я писал выше.

По популярности это топовая модель как среди исследователей, которые любят ее за простоту и интерпретируемость (коэффициенты такие же, как у линейной регрессии), так и среди инженеров. На очень больших нагрузках, в отличие от других классификаторов, эта простая формула легко масштабируется. И когда вас догоняет в интернете баннерная реклама, скорее всего, за ней стоит логистическая регрессия, которая до недавнего времени использовалась, например, в компании Criteo, одной из самых больших ретаргетинговых компаний в мире [54].