Роман Зыков - Роман с Data Science. Как монетизировать большие данные [litres]

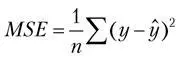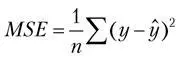
Есть еще ряд популярных метрик, таких как RMSE, MAE, R2.

Для задач классификации самые популярные метрики можно легко получить из матрицы ошибок классификации (misclassification или confusion matrix). Когда я собеседую кандидата на должность аналитика, то часто прошу нарисовать эту матрицу (табл. 8.2) и вывести из нее метрики.

Представьте, что вам нужно решить задачу классификации – определить, простужен человек или нет. У вас есть датасет со следующими фичами: температура тела, болит ли горло, есть ли насморк, чихание, светобоязнь. Для каждого примера у вас есть идентификатор: 1, или True, – человек болен простудой, 0, или False, – нет. Вы строите модель, которая для каждого примера дает результат: 1 для больного, 0 для здорового. Чтобы понять ошибку вашей модели, нужно сравнить ее вывод и правильные значения. Допустим, мы это сделали и теперь можем составить такую матрицу ошибок классификации. В строках мы отметим предсказанные значения, в столбцах – действительные. В ячейках таблицы можем написать количество случаев для каждого класса (0 и 1) – когда прогноз совпал, а когда нет. Я заполнил таблицу, к примеру, 100 примеров, когда мы верно угадали единицу.

Таблица 8.2. Матрица ошибок классификации

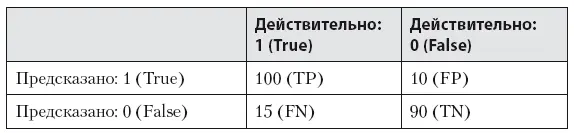
В скобках написаны обозначения, которые нам пригодятся для вывода метрик: TP = True Positive (правильно угаданные 1), TN = True Negative (правильно угаданные 0), FN = False Negative (ложно негативные, модель посчитала 0, а на самом деле 1), FP = False Positive (модель посчитала 1, а на деле 0). Давайте выведем метрики:

Accuracy (Точность) = точно угаданные / число примеров =

= (TP + TN) / (TP + TN + FP + FN).

Precision (Точность для 1) = TP / (TP + FP).

Recall (Полнота) = TP / (TP + FN) (или сколько процентов 1 мы нашли правильно).

F мера = 1 / (1/Precision + 1/Recall).

Самые часто применяющиеся метрики для классификации – precision и recall. Они не зависят от несбалансированности классов, как accuracy. Эта ситуация возникает, когда соотношение единиц и нулей в датасете далеко от 50/50.

В метриках классификации есть еще одна интересная – AUC-ROC (Area Under Curve of Receiver Operating Characteristic). Она нужна тогда, когда алгоритм классификации выдает вероятность принадлежности к какому-либо классу – 0 или 1. Чтобы посчитать метрики Recall и Precision, нам придется делать разные пороговые значения для вероятностей (чтобы различать классы) и считать их. Как раз для этого и нужна AUC-ROC, которая хорошо показывает эффективность классификатора независимо от порогового значения. Чтобы ее построить, необходимо взять набор пороговых значений из отрезка [8–0;1] и для каждого значения порога вычислить два числа:

TPR (True Positive Rate) = TP/(TP + FN) и

FPR (False Positive Rate) = FP/(FP + TN).

Отметить эти числа как точки в плоскости координат TPR и FPR и получить следующую кривую (рис. 8.3).

Площадь под ней и есть AUC. В случае если вы получаете AUC близкий к 0.5, ваш классификатор почти ничем не отличается от

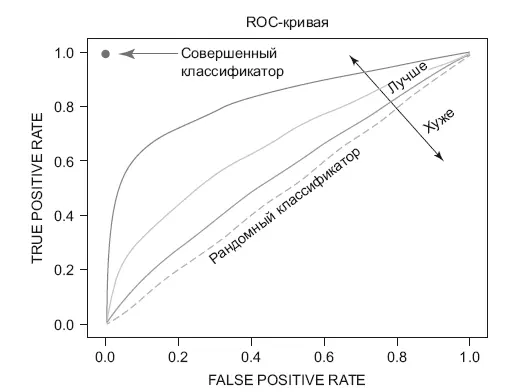
Рис. 8.3.ROC-кривая

случайного подбрасывания монетки. Чем его значение ближе к 1, тем лучше. Этот показатель часто используется в научной литературе и соревнованиях Kaggle.

Для других задач, например для ранжирования результатов поиска и для рекомендаций, используются свои показатели качества работы, о них можно узнать в специальной литературе.

Итак, у нас есть метрика. Теперь с ее помощью мы сможем сравнивать разные модели друг с другом и понимать, какая из них лучше. Можно приступать к обучению.

Практически любая ML-модель для обучения с учителем сводится к двум вещам: определение функции потерь (loss function для одного примера, cost function для множества примеров) и процедуры ее минимизации.

Например, для линейной регрессии это будет среднеквадратичная ошибка в том виде, в каком мы определили ее ранее. Чтобы найти минимум функции потерь, существуют различные процедуры оптимизации. Одна из них называется градиентным спуском (Gradient Descent), она широко применяется на практике.

Как правило, оптимизация выглядит следующим образом:

1. Коэффициенты (которые нужно подобрать) модели инициализируются нулями или случайно.

2. Вычисляется величина функции потерь (например, среднеквадратичное отклонение) и ее градиент (производная от функции потерь). Градиент нам нужен, чтобы понять, куда двигаться для минимизации ошибки.