Эндрю Уэзеролл - Компьютерные сети. 5-е издание

Предполагается, что маршрутизаторам известно расстояние до каждого из соседей. Если в качестве единицы измерения используется число транзитных участков, то расстояние равно одному транзитному участку. Если же дистанция измеряется временем задержки распространения, то маршрутизатор может измерить его с помощью специального пакетаECHO (эхо), в который получатель помещает время получения и который отправляет обратно как можно быстрее.

Предположим, что в качестве единицы измерения используется время задержки и этот параметр относительно каждого из соседей известен маршрутизатору. Через каждые T мс все маршрутизаторы посылают своим соседям список с приблизительными задержками для каждого получателя. Они, разумеется, также получают подобный список от всех своих соседей. Допустим, одна из таких таблиц пришла от соседа X и в ней указывается, что время распространения от маршрутизатора X до маршрутизатора i равно Xi. Если маршрутизатор знает, что время пересылки до маршрутизатора X равно m, тогда задержка при передаче пакета маршрутизатору i через маршрутизатор X составит Xi + m. Выполнив такие расчеты для всех своих соседей, маршрутизатор может выбрать наилучшие пути и поместить соответствующие записи в новую таблицу. Обратите внимание, что старая таблица в расчетах не используется.

Процесс обновления таблицы проиллюстрирован на рис. 5.7. На рис. 5.7, а показана сеть. Первые четыре столбца на рис. 5.7, б показывают векторы задержек, полученные маршрутизатором J от своих соседей. Маршрутизатор A считает, что время пересылки от него до маршрутизатора B равно 12 мс, 25 мс до маршрутизатора C, 40 мс до D и т. д. Предположим, что маршрутизатор J измерил или оценил задержки до своих соседей A, I, H и K как 8, 10, 12 и 6 мс соответственно.

Теперь рассмотрим, как J рассчитывает свой новый маршрут к маршрутизатору G. Он знает, что задержка до A составляет 8 мс и при этом A думает, что от него до G данные дойдут за 18 мс. Таким образом, J знает, что если он станет отправлять пакеты для G через A, то задержка составит 26 мс. Аналогично, он вычисляет значения задержек для маршрутов от него до G, проходящих через остальных его соседей (I, H и K), и получает соответственно 41 (31 + 10), 18 (6+12) и 37 (31+6). Лучшим значением является 18, поэтому именно оно помещается в таблицу в запись для получателя G. Вместе с числом 18 туда же помещается обозначение линии, по которой

проходит самый короткий маршрут до G, то есть H. Данный метод повторяется для всех остальных адресатов, и при этом получается новая таблица, показанная в виде правого столбца на рисунке.

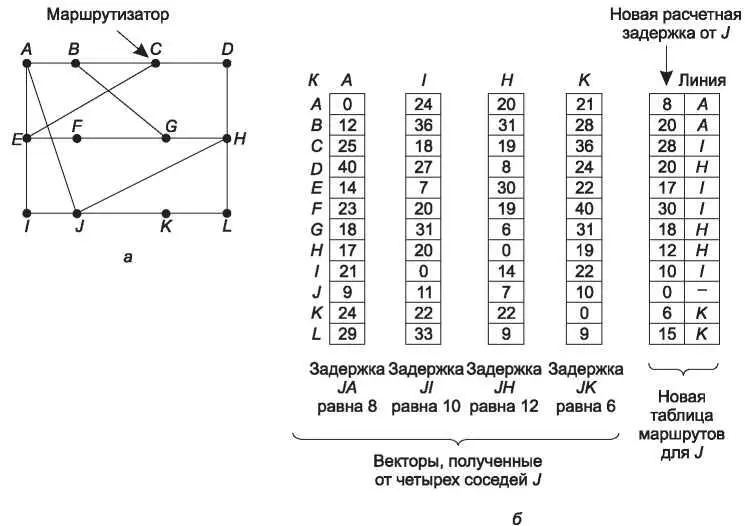
Рис. 5.7. Сеть (а); полученные от A, I, H и K векторы и новая таблица маршрутов для J (б)

Проблема счета до бесконечности

Установление маршрутов, соответствующих кратчайшим путям, в сети называется конвергенцией( convergence). Алгоритм маршрутизации по вектору расстояний — простой метод, позволяющий маршрутизаторам совместно вычислять кратчайшие пути. Однако на практике он обладает серьезным недостатком: хотя правильный ответ в конце концов и находится, процесс его поиска может занять довольно много времени. В частности, такой алгоритм быстро реагирует на хорошие новости и очень лениво — на плохие. Рассмотрим маршрутизатор, для которого расстояние до маршрутизатора X достаточно велико. Если при очередном обмене векторами его сосед A сообщит ему, что от него до маршрутизатора X совсем недалеко, наш маршрутизатор просто переключится для передач маршрутизатору X на линию, проходящую через этого соседа. Таким образом, хорошая новость распространилась всего за один обмен информацией.

Чтобы увидеть, как быстро распространяются хорошие известия, рассмотрим линейную сеть из пяти узлов, показанную на рис. 5.8, в которой мерой расстояния служит количество транзитных участков. Предположим, что вначале маршрутизатор A выключен, и все остальные маршрутизаторы об этом знают. То есть они считают, что расстояние до A равно бесконечности.