Эндрю Уэзеролл - Компьютерные сети. 5-е издание

Прямым следствием принципа оптимальности является возможность рассмотрения множества оптимальных маршрутов от всех источников к конкретным приемникам в виде дерева, имеющего приемник в качестве корня. Такое дерево называется входным деревом (sink tree). Оно изображено на рис. 5.5, б. Расстояния измеряются количеством транзитных участков. Цель всех алгоритмов выбора маршрутов заключается в вычислении и использовании входных деревьев для всех маршрутизаторов.

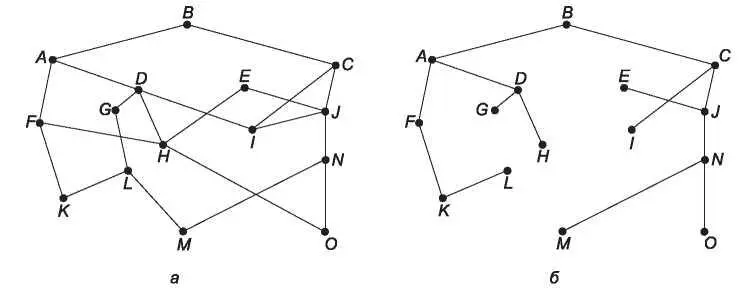
Рис. 5.5.Сеть (а); входное дерево для маршрутизатора B (б)

Обратите внимание на то, что входное дерево не обязательно является уникальным; у одной сети может существовать несколько деревьев с одинаковыми длинами путей. Если мы будем считать все возможные пути допустимыми, мы получим более общую структуру, и наше дерево будет подходить под определение направленного ациклического графа( directed acyclic graph, DAG). В таких графах нет циклов. Мы будем использовать понятие входного дерева для обозначения обоих вариантов. Оба они также основываются на предположении, что пути не мешают друг другу (из этого следует, в частности, что появление затора на одном пути не приводит к изменению другого пути).

Поскольку входное дерево действительно является деревом, оно не содержит петель, поэтому каждый пакет будет доставлен за конечное и ограниченное число пересылок. На практике все это не так просто. Линии связи и маршрутизаторы могут выходить из строя и снова появляться в сети во время выполнения операции, поэтому у разных маршрутизаторов могут оказаться различные представления о текущей топологии сети. Кроме того, мы обошли вопрос о том, собирает ли маршрутизатор сам информацию для вычисления входного дерева, или эта информация каким-то другим образом поступает к нему. Мы вскоре рассмотрим этот вопрос. Тем не менее принцип оптимальности и входное дерево — это те точки отсчета, относительно которых можно измерять эффективность различных алгоритмов маршрутизации.

5.2.2. Алгоритм нахождения кратчайшего пути

Начнем наше изучение алгоритмов выбора маршрутов с простого метода вычисления кратчайших путей, требующего полной информации о сети. Целью распределенного алгоритма является нахождение таких путей даже в тех случаях, когда маршрутизатор не располагает всеми сведениями о сети.

Идея заключается в построении графа сети, в котором каждый узел будет соответствовать маршрутизатору, а каждое ребро — линии связи или просто связи. При выборе маршрута между двумя маршрутизаторами алгоритм просто находит кратчайший путь между ними на графе.

Концепция кратчайшего пути( shortest path) требует некоторого пояснения. Один из способов измерения длины пути состоит в подсчете количества транзитных участков. В таком случае пути ABC и ABE на рис. 5.6 имеют одинаковую длину. Можно измерять расстояния в километрах. В таком случае окажется, что путь ABC значительно длиннее пути ABE (предполагается, что рисунок изображен с соблюдением масштаба).

Однако, помимо учета количества транзитных участков и физической длины линий, возможен учет и других параметров. Например, каждому ребру графа можно поставить в соответствие среднее время задержки стандартного тестового пакета, измеряемое каждый час. В таком графе кратчайший путь определяется как самый быстрый путь, а не путь с наименьшим числом ребер или наименьшей длиной в километрах.

В общем случае параметры ребер графа являются функциями расстояния, пропускной способности, средней загруженности, стоимости связи, измеренной величины задержки и других факторов. Изменяя весовую функцию, алгоритм может вычислять кратчайший путь с учетом любого количества критериев в различных комбинациях.

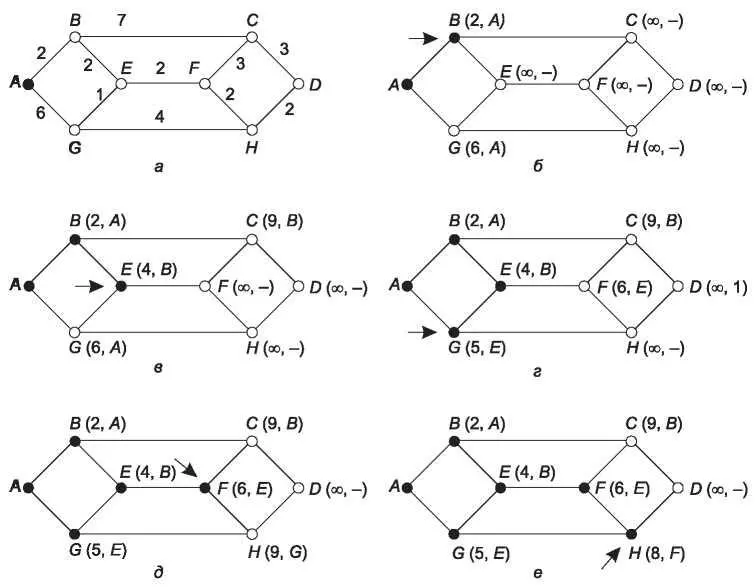
Рис. 5.6.Первые шесть шагов вычисления кратчайшего пути от A к D. Стрелка указывает на рабочий узел

Известно несколько алгоритмов вычисления кратчайшего пути между двумя узлами графа. Один из них был создан знаменитым Дейкстрой (Dijkstra) в 1959 году. Он находит кратчайшие пути между отправителем и всеми возможными адресами назначения в данной сети. Каждый узел помечается (в скобках) расстоянием до него от узла отправителя по наилучшему известному пути. Эти расстояния должны быть неотрицательными; если они основаны на реальных величинах — таких как пропускная способность и время задержки, — это условие будет выполнено. Вначале пути неизвестны, поэтому все узлы помечаются символом бесконечности. По мере работы алгоритма и нахождения путей отметки узлов изменяются, показывая оптимальные пути. Отметка может быть постоянной или экспериментальной. Вначале все отметки являются ориентировочными. Когда выясняется, что отметка действительно соответствует кратчайшему возможному пути, она становится постоянной и в дальнейшем не изменяется.