Эндрю Уэзеролл - Компьютерные сети. 5-е издание

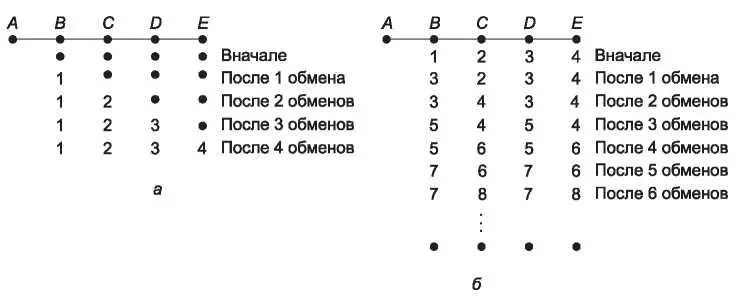
Рис. 5.8. Проблема счета до бесконечности

Когда в сети появляется A, остальные маршрутизаторы узнают об этом с помощью обмена векторами. Для простоты будем предполагать, что где-то в сети имеется гигантский гонг, в который периодически ударяют, чтобы инициировать одновременный обмен векторами. После первого обмена B узнает, что у его соседа слева нулевая задержка при связи с A, а B помечает в своей таблице маршрутов, что A находится слева на расстоянии одного транзитного участка. Все остальные маршрутизаторы в этот момент еще полагают, что A выключен. Значения задержек для A в таблицах на этот момент показаны во второй строке на рис. 5.8, а. При следующем обмене информацией C узнает, что у B есть путь к A длиной 1, поэтому он обновляет свою таблицу, указывая длину пути до A, равную 2, но D и E об этом еще не знают. Таким образом, хорошие вести распространяются со скоростью один транзитный участок за один обмен векторами. Если самый длинный путь в сети состоит из N транзитных участков, то через N обменов все маршрутизаторы подсети будут знать о включенных маршрутизаторах и заработавших линиях.

Теперь рассмотрим ситуацию на рис. 5.8, б, в которой все связи и маршрутизаторы изначально находятся во включенном состоянии. Маршрутизаторы B, C, D и E находятся на расстоянии 1, 2, 3 и 4 транзитных участков от A соответственно. Внезапно либо A отключается, либо происходит обрыв линии между A и B (что с точки зрения B одно и то же).

При первом обмене пакетами B не слышит ответа от A. К счастью, C говорит: «Не волнуйся. У меня есть путь к A длиной 2». B вряд ли догадывается, что путь от C к A проходит через B. B может только предполагать, что у C около 10 выходных связей с независимыми путями к A, кратчайшая из которых имеет длину 2. Поэтому теперь B думает, что может связаться с A через C по пути длиной 3. При этом первом обмене маршрутизаторы D и E не обновляют свою информацию об A.

При втором обмене векторами C замечает, что у всех его соседей есть путь к A длиной 3. Он выбирает один из них случайным образом и устанавливает свое расстояние до A равным 4, как показано в третьей строке на рис. 5.8, б. Результаты последующих обменов векторами также показаны на этом рисунке.

Теперь должно быть понятно, почему плохие новости медленно распространяются — ни один маршрутизатор не может установить значение расстояния, более чем на

единицу превышающее минимальное значение этого расстояния, хранящееся у его соседей. Таким образом, все маршрутизаторы будут до бесконечности увеличивать значение расстояния до выключенного маршрутизатора. Количество необходимых для завершения этого процесса обменов векторами можно ограничить, если установить значение этой «бесконечности» равным длине самого длинного пути плюс 1.

Неудивительно, что эта проблема называется счетом до бесконечности (count-to-infinity). Было сделано много попыток решить ее, например можно запретить маршрутизатору сообщать о своих кратчайших путях соседям, от которых они получили эту информацию, с помощью правила расколотого горизонта с «отравляющим» ответом внесенного в RFC 1058. Однако на практике все эти эвристические правила с красивыми названиями оказались абсолютно бесполезными. Суть проблемы заключается в том, что когда Х сообщает Y о том, что у него есть какой-то путь, у Y нет никакой возможности узнать, входит ли он сам в этот путь.

5.2.5. Маршрутизация с учетом состояния линий

Маршрутизация на основе векторов расстояний использовалась в сети ARPANET вплоть до 1979 года, когда ее сменил алгоритм маршрутизации с учетом состояния линий. Отказаться от прежнего алгоритма пришлось в первую очередь потому, что при изменении топологии сети алгоритм слишком долго приходил к устойчивому состоянию (вследствие проблемы счета до бесконечности). В результате он был заменен на совершенно новый алгоритм, ныне называемый маршрутизацией с учетом состояния линий (link state routing). Сейчас в крупных сетях и сети Интернет используются его варианты — алгоритмы маршрутизации IS-IS и OSPF.

В основе алгоритма лежит относительно простая идея, ее можно изложить в пяти требованиях к маршрутизатору. Каждый маршрутизатор должен: