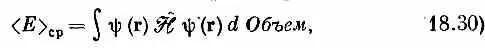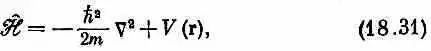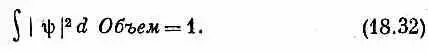Поэтому можно написать
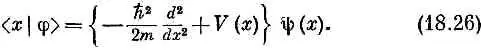
Вспомним, что x >=< x |y>*=y*( x ); с помощью этого равенства среднее значение энергии в (18.23) можно записать в виде
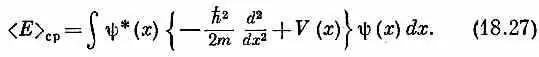
Если волновая функция y ( x ) известна, то, взяв этот интеграл, вы получите среднюю энергию. Вы теперь начинаете понимать, как от представлений о волновом векторе можно перейти к представлению о волновой функции и обратно.
Величина в фигурных скобках в (18.27) это алгебраический оператор. [«Оператор» V ( x ) означает «умножь на V ( x ) ». ] Мы обозначим его 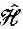
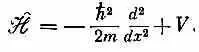
В этих обозначениях (18.23) превращается в
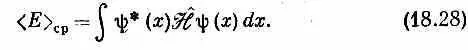
Определенный здесь алгебраический оператор 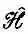 , конечно, не тождествен с квантовомеханическим оператором Н ^ . Новый оператор действует на функцию координаты y( x )=< x |y>, образуя новую функцию от х, j( x )=< x |j>, а H ^ действует на вектор состояния |y>, образуя другой вектор состояния |ф>, причем не имеется в виду ни координатное, ни вообще какое-либо частное представление. Мало того, даже в координатном представлении
, конечно, не тождествен с квантовомеханическим оператором Н ^ . Новый оператор действует на функцию координаты y( x )=< x |y>, образуя новую функцию от х, j( x )=< x |j>, а H ^ действует на вектор состояния |y>, образуя другой вектор состояния |ф>, причем не имеется в виду ни координатное, ни вообще какое-либо частное представление. Мало того, даже в координатном представлении 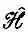 не совсем то же, что Н ^ . Если бы мы решили работать в координатном представлении, то смысл оператору H ^ пришлось бы придавать с помощью матрицы < x | H ^| x '>, которая как-то зависит от двух «индексов» x и x '; иначе говоря, следовало бы ожидать, что [как утверждает (18.25)] < x |j> связано со всеми амплитудами < x |y> операцией интегрирования. А с другой стороны, мы нашли, что
не совсем то же, что Н ^ . Если бы мы решили работать в координатном представлении, то смысл оператору H ^ пришлось бы придавать с помощью матрицы < x | H ^| x '>, которая как-то зависит от двух «индексов» x и x '; иначе говоря, следовало бы ожидать, что [как утверждает (18.25)] < x |j> связано со всеми амплитудами < x |y> операцией интегрирования. А с другой стороны, мы нашли, что 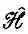 — это дифференциальный оператор. Связь между < x | H ^| х' > и алгебраическим оператором
— это дифференциальный оператор. Связь между < x | H ^| х' > и алгебраическим оператором 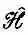
мы уже выясняли в гл. 14, § 5.
Наши результаты нуждаются в одном уточнении. Мы предположили, что амплитуда y ( x )=< x |y> нормирована, т, е. масштабы выбраны так, что
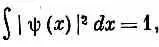
и вероятность увидеть электрон все равно где равна единице. Но вы могли бы, если бы захотели работать с ненормированной y ( х ) , следовало бы только писать
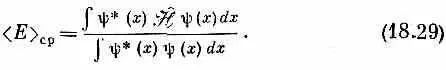
Это одно и то же.
Обратите внимание на сходство между (18.28) и (18.18). Оба эти способа записи одного и того же результата при работе в x -представлении часто встречаются. От первого можно перейти ко второму, если А ^ — локальный оператор, т. е. такой, для которого интеграл
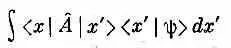
может быть записан в виде 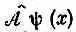 , где
, где 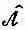 — дифференциальный алгебраический оператор. Однако встречаются операторы, для которых это неверно. Тогда приходится работать с исходными уравнениями (18.21) и (18.22).
— дифференциальный алгебраический оператор. Однако встречаются операторы, для которых это неверно. Тогда приходится работать с исходными уравнениями (18.21) и (18.22).
Наш вывод легко обобщается на три измерения. Итог таков:
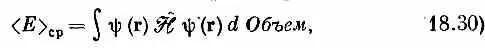
где
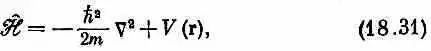
причем подразумевается, что
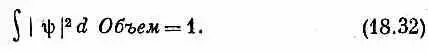
Такие же уравнения получаются довольно очевидным образом и при обобщении на системы с несколькими электронами, но мы не будем сейчас заниматься выписыванием результатов.
Читать дальше

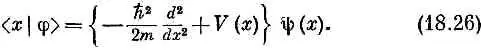
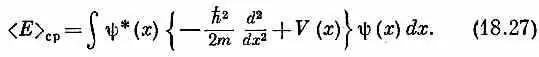
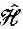
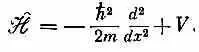
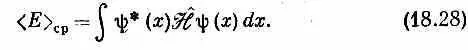
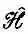 , конечно, не тождествен с квантовомеханическим оператором Н ^ . Новый оператор действует на функцию координаты y( x )=< x |y>, образуя новую функцию от х, j( x )=< x |j>, а H ^ действует на вектор состояния |y>, образуя другой вектор состояния |ф>, причем не имеется в виду ни координатное, ни вообще какое-либо частное представление. Мало того, даже в координатном представлении
, конечно, не тождествен с квантовомеханическим оператором Н ^ . Новый оператор действует на функцию координаты y( x )=< x |y>, образуя новую функцию от х, j( x )=< x |j>, а H ^ действует на вектор состояния |y>, образуя другой вектор состояния |ф>, причем не имеется в виду ни координатное, ни вообще какое-либо частное представление. Мало того, даже в координатном представлении 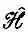 не совсем то же, что Н ^ . Если бы мы решили работать в координатном представлении, то смысл оператору H ^ пришлось бы придавать с помощью матрицы < x | H ^| x '>, которая как-то зависит от двух «индексов» x и x '; иначе говоря, следовало бы ожидать, что [как утверждает (18.25)] < x |j> связано со всеми амплитудами < x |y> операцией интегрирования. А с другой стороны, мы нашли, что
не совсем то же, что Н ^ . Если бы мы решили работать в координатном представлении, то смысл оператору H ^ пришлось бы придавать с помощью матрицы < x | H ^| x '>, которая как-то зависит от двух «индексов» x и x '; иначе говоря, следовало бы ожидать, что [как утверждает (18.25)] < x |j> связано со всеми амплитудами < x |y> операцией интегрирования. А с другой стороны, мы нашли, что 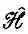 — это дифференциальный оператор. Связь между < x | H ^| х' > и алгебраическим оператором
— это дифференциальный оператор. Связь между < x | H ^| х' > и алгебраическим оператором 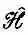
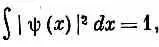
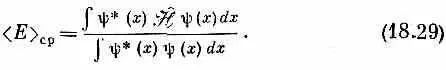
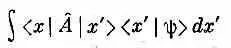
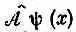 , где
, где 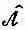 — дифференциальный алгебраический оператор. Однако встречаются операторы, для которых это неверно. Тогда приходится работать с исходными уравнениями (18.21) и (18.22).
— дифференциальный алгебраический оператор. Однако встречаются операторы, для которых это неверно. Тогда приходится работать с исходными уравнениями (18.21) и (18.22).