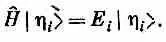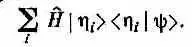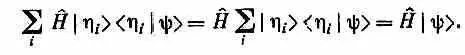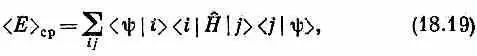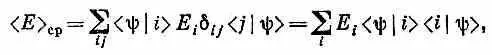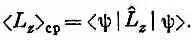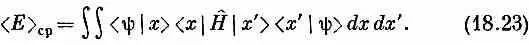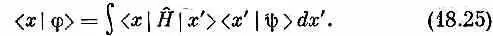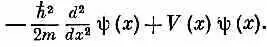Но вспомним теперь, что такое |h i >. Состояния |h i > считаются стационарными, т. е. для каждого из них
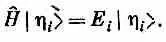
А раз Е i — просто число, то правая часть совпадает с |h i > Е i , а сумма в (18.16) — с
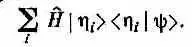
Теперь приходится просуммировать по i общеизвестную комбинацию, приводящую к единице:
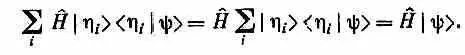
Чудесно, уравнение (18.16) совпало с

Средняя энергия состояния |y> записывается, стало быть, в очень привлекательном виде

Чтобы получить среднюю энергию, подействуйте на |y> оператором Н ^ и затем умножьте на какую угодно совокупность базисных состояний, и, если мы знаем гамильтонову матрицу Н ij для этой совокупности, мы уже сможем узнать среднюю энергию. Уравнение (18.18) говорит, что при любой совокупности базисных состояний | i > средняя энергия может быть вычислена из
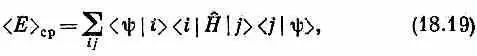
где амплитуды < i | H | j > как раз и есть элементы матрицы H ij . Проверим это на том частном примере, когда состояния | i > суть состояния с определенной энергией. Для них H ^| j >= e | j >, так что < i | H ^| j >= E j d ij и
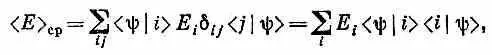
что вполне естественно.
Уравнение (18.19) можно, кстати, обобщить и на другие физические измерения, которые вы в состоянии выразить в виде оператора. Например, пусть L ^ z есть оператор z -компоненты момента количества движения L. Средняя z -компонента для состояния |y> равна
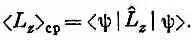
Один из способов доказательства этой формулы — придумать такую задачу, в которой энергия пропорциональна моменту количества движения. Тогда все рассуждения просто повторятся. Подытоживая, скажем, что если физически наблюдаемая величина А связана с соответствующим квантовомеханическим оператором А ^ , то среднее значение А в состоянии |y> дается формулой

Под этим подразумевается

где

§ 3. Средняя энергия атома
Пусть мы хотим узнать среднюю энергию атома в состоянии, описываемом волновой функцией y( r); как же ее найти? Рассмотрим сперва одномерную задачу, когда состояние |y> определяется амплитудой < x |y>=y ( x ). Нас интересует частный случай применения уравнения (18.19) к координатному представлению. Следуя нашей обычной процедуре, заменим состояния | i > и | j > на | х > и | х' > и сумму на интеграл. Мы получим
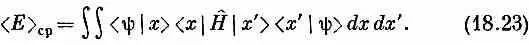
Этот интеграл можно при желании записывать иначе:

где
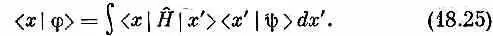
Интеграл по х' в (18.25) тот же самый, что встречался нам в гл. 14 [см. (14.50) и (14.52)]. Он равен
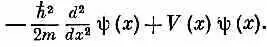
Читать дальше