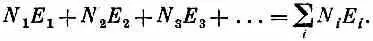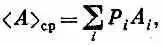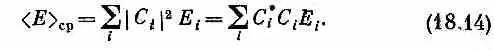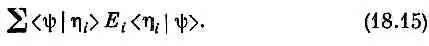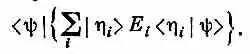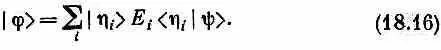Feynmann - Feynmann 9

Но что случится, если вы проделаете свои измерения над состоянием |y>, которое не является стационарным? Раз у си­стемы нет определенной энергии, то одно измерение даст одну энергию, то же измерение над другим атомом в том же состоя­нии даст другую и т. д. Каким же окажется среднее всей серии измерений энергии?

На этот вопрос мы ответим, если возьмем проекцию состоя­ния |y> на систему состояний с определенной энергией. Чтобы помнить, что это особый базис, будем обозначать эти состояния |h i >. Каждое из состояний |h i > обладает определенной энер­гией E i , В этом представлении

Когда вы проделываете измерение энергии и получаете некото­рое число Е i , вы тем самым обнаруживаете, что система была в состоянии |h i >. Но в каждом новом измерении вы можете получить новое число. Иногда вы получите E 1 , иногда Е 2 , иногда Е 3 и т. д. Вероятность, что вы обнаружите энергию E 1?равна попросту вероятности обнаружить систему в состоянии |h 1>, т. е. квадрату модуля амплитуды С 1=1|y>. Вероятность обнаружить то или иное возможное значение энергии E i есть

P i = | C i | 2. (18.11)

Как же связать эти вероятности со средним значением всей последовательности измерений энергий? Вообразим, что мы получили ряд результатов измерений, например E 1 , Е 7 , E 11 , Е 9 , E 1, E 10 , Е 7 , E 2 , Е 3 , Е 9 , Е 6 , E 4 и т. д., всего тысяча измерений. Сложим все энергии и разделим на 1000. Это и есть среднее. Можно сложение проделать и покороче. Посчитайте, сколько раз у вас вышло E 1 (скажем, оно вышло N 1 раз), сколько раз вышло Е 2 (скажем, N 2 раз) и т. д. Ясно, что сумма всех энер­гий равна

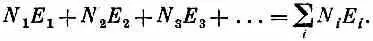
Средняя энергия равна этой сумме, деленной на полное число измерений, т. е. на сумму всех N i , которую мы обозначим N :

Мы почти у цели. Под вероятностью какого-нибудь собы­тия мы понимаем как раз число случаев, когда ожидается на­ступление этого события, деленное на общее число испытаний. Отношение N i / N должно (при больших N ) мало отличаться от P i — вероятности обнаружить состояние |h i >, хоть и не будет точно совпадать с Р i из-за статистических флуктуации. Обозначим предсказываемую (или «ожидаемую») среднюю энер­гию < E > ср; тогда мы вправе сказать

Те же рассуждения подойдут к измерениям каких угодно вели­чин. Среднее значение измеряемой величины А должно равняться

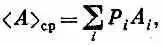
где a i — различные допустимые значения наблюдаемой вели­чины, а Р i — вероятность получения этого значения.

Вернемся теперь к нашему квантовомеханическому состо­янию |y>. Его средняя энергия равна

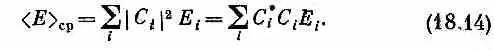
А теперь следите внимательно! Сначала перепишем эту сумму так:

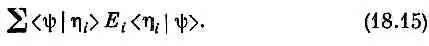
Теперь будем рассматривать левое

Вынесем его за знак суммы и напишем

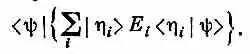
Это выражение имеет вид , где |j> — некоторое «придуманное» состояние, определяемое равенством

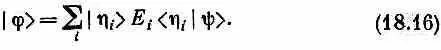
Иными словами, это то состояние, которое у вас получится, если вы возьмете каждое базисное состояние |h i > в количестве

Е i i |y>.