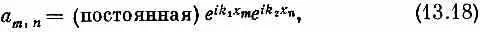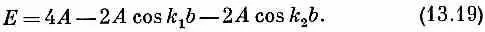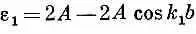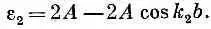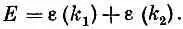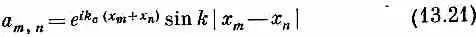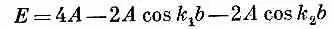Feynmann - Feynmann 9

Теперь уже решение отыскать нетрудно. Мы немедленно по­лучаем

где

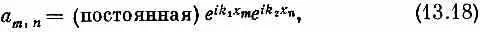
а

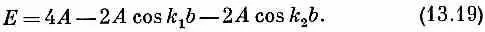
Поразмыслим минутку о том, что было бы, если бы у нас были две независимые, отдельные спиновые волны (как в пре­дыдущем параграфе), соответствующие k = k 1 и k = k 2; их энер­гии из (13.12) имели бы вид

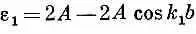
и

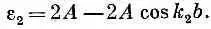
Заметьте, что энергия Е в (13.19) является как раз их суммой:

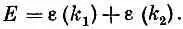
Иными словами, наше решение можно толковать следующим образом. Имеются две частицы, т. е. пара спиновых волн, одна из которых обладает импульсом, описываемым числом k 1 a другая — числом k 2; энергия системы равна сумме энергий этих двух объектов. Обе частицы действуют совершенно независи­мо. Вот и все, что в этом есть — и ничего больше.

Конечно, мы сделали некоторые приближения, но в данный момент мы не будем обсуждать точность нашего ответа. Вы, однако, чувствуете, что в кристаллах разумного размера с миллиардами атомов и, стало быть, с миллиардами слагаемых в гамильтониане большой ошибки от пренебрежения немногими слагаемыми не выйдет. Если бы, конечно, перевернутых спинов стало так много, что их плотность была бы заметной, то при­шлось бы позаботиться и о поправках.

(Интересно, что в случае, когда перевернутых спинов только два, можно написать и точное решение. Но результат особой важности не представляет. Просто интересно, что в этом случае уравнения можно решить точно. Решение таково:

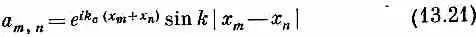
с энергией

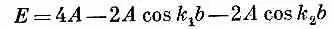
и с волновыми числами k c и k , связанными с k 1и k 2 формулами

k 1= k c - k , k 2 = k c + k . (13.22)

В этом решении отражено и «взаимодействие» пары спинов. Оно описывает тот факт, что когда спины сближаются, возникает какая-то вероятность их рассеяния. Поведение спинов очень по­хоже на взаимодействие частиц. Но подробная теория их рас­сеяния выходит за пределы того, о чем мы здесь собрались го­ворить.)

§ 3. Независимые частицы

В предыдущем параграфе мы написали гамильтониан (13.15) для двухчастичной системы. Затем, пользуясь приближением, эквивалентным пренебрежению каким-либо «взаимодействием» между двумя частицами, мы нашли стационарные состояния, описываемые формулами (13.17) и (13.18). Это состояние по­просту есть произведение двух одночастичных состояний. Но решение, которое мы написали для а m , n [формула (13.18)], на самом деле удовлетворить нас не может. Мы с самого начала подчеркивали, что состояние | х 9 , x 4> не отличается от состоя­ния | x 4 , x 9), что порядок х m и х n неважен. Вообще говоря, алгеб­раическое выражение для амплитуды С m , n не должно меняться от перестановки значений х m и х n , потому что она не изменяет состояния. В любом случае она будет представлять амплитуду того, что спин, направленный вниз, обнаружится в х m и в х n .

Но обратите внимание, что (13.18) несимметрично по х m и х n , поскольку k 1 и k 2, вообще говоря, различны.

Все дело в том, что мы не заставили наше решение (13.15) подчиниться этому добавочному условию. К счастью, пока не­трудно все исправить. Заметьте, во-первых, что ничуть не хуже формулы (13.18) другое решение уравнения Гамильтона:

И даже энергия здесь та же самая, что была в (13.18). Значит, любая линейная комбинация (13.18) и (13.23) также будет ре­шением системы и будет обладать по-прежнему энергией, давае­мой (13.19). Решение, которое нужно выбрать по требованиям симметрии,—просто сумма (13.18) и (13.23):