Feynmann - Feynmann 9

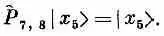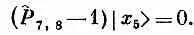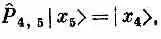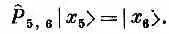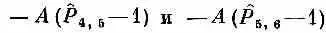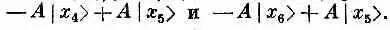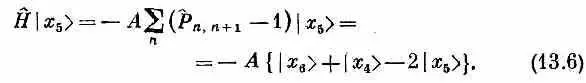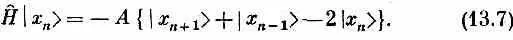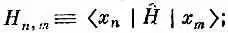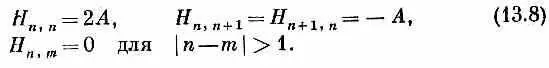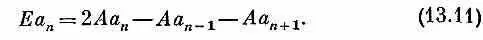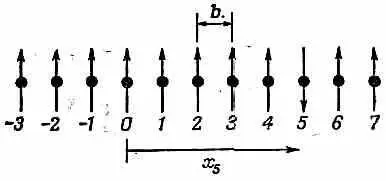
Фиг. 13.1. Базисное состояние | x 5> системы спинов, расположенных по одной линии.

Все спины направлены вверх, а тот, что в х 5 , перевернут.

Вообще, | х n > будет обозначать состояние с одним перевернутым спином, рас­положенным в координате х n n -го атома.

Как же действует гамильтониан (13.5) на состояние | x 5>? Один из членов гамильтониана это, скажем, — А (Р ^ 7 ,8 -1). Оператор P^ 7,8обменивает спинами два соседних атома № 7 и № 8. Но в состоянии | x 5> они оба направлены вверх, так что ничего не меняется; Р^ 7 , 8равнозначно умножению на единицу:

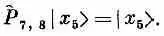
Отсюда следует

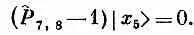
Стало быть, все члены гамильтониана, кроме тех, куда вхо­дит атом № 5, дадут нуль. Операция P^ 4,5, действуя на со­стояние | x 5>, обменивает спинами атом № 4 (со спином вверх) и атом № 5 (со спином вниз). В результате появляется со­стояние, в котором все спины смотрят вверх, кроме атома в точке 4. Иначе говоря,

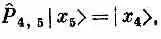
Точно так же

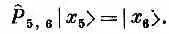
Значит, изо всего гамильтониана выживут только члены

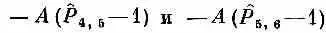
Действуя на |x 5>, они дадут соответственно

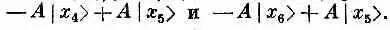
В итоге

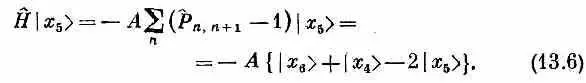
Когда гамильтониан действует на состояние | x 5>, то возни­кает некоторая амплитуда оказаться в состояниях | x 4> и | х 6> . Это просто означает, что существует определенная амплитуда того, что направленный книзу спин перепрыгнет к соседнему атому. Значит, из-за взаимодействия между спинами, если вна­чале один спин был направлен вниз, имеется некоторая ве­роятность того, что позднее вместо него вниз будет смотреть другой. При действии на состояние | х n > гамильтониан дает

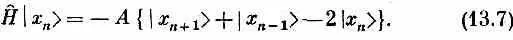
Заметьте, в частности, что если взять полную систему состоя­ний только с одним спином-«перевертышем», то они будут перемешиваться только между собой. Гамильтониан никогда не перемешает эти состояния с другими, в которых спинов-«перевертышей» больше. Пока вы только обмениваетесь спинами, вы никогда не сможете изменить общего количества перевертышей. Удобно будет использовать для гамильтониана матричное обозначение, скажем,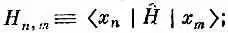

уравнение (13.7) эквивалентно следующему:

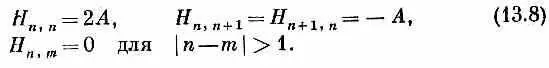
Каковы же теперь уровни энергии для состояний с одним перевернутым спином? Пусть, как обычно, С n — амплитуда того, что некоторое состояние |y> находится в состоянии | x n >. Если мы хотим, чтобы |y> было состоянием с определенной энергией, то все С n обязаны одинаково меняться со временем, а именно по правилу

Подставим это пробное решение в наше обычное уравнение Гамильтона

используя в качестве матричных элементов (13.8). Мы, конечно, получим бесконечное количество уравнений, но все их можно будет записать в виде

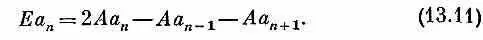
Перед нами опять в точности та же задача, что и в гл. 11, только там, где раньше стояло Е 0 , теперь стоит 2 А. Решения отвечают амплитудам С n (амплитудам с перевернутым спином), которые распространяются вдоль решетки с константой распростране­ния k и энергией