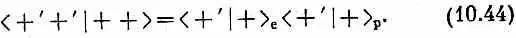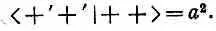Feynmann - Feynmann 8a

Таблица 10.3 · СОСТОЯНИЯ АТОМА ВОДОРОДА В НУЛЕВОМ ПОЛЕ

§ 6. Проекционная матрица для спина 1

Теперь мы хотели бы применить наши знания об атоме водо­рода к одной специальной задаче. В гл. 3 мы говорили о том, что частица со спином 1, находящаяся в одном из базисных со­стояний (+, 0, -) по отношению к прибору Штерна — Герлаха с какой-то частной ориентацией (скажем, по отношению к при­бору S), будет иметь определенную амплитуду пребывания в одном из трех состояний по отношению к прибору Т, ориенти­рованному в пространстве по-другому. Имеются девять таких амплитуд < jT | iS > , которые вместе образуют проекционную матрицу. В гл. 3, § 7, мы без доказательства выписали элементы этой матрицы для различных ориентации Т по отношению к S. Теперь мы хотим показать вам один из способов их вывода.

В атоме водорода мы с вами отыскали систему со спином 1, составленную из двух частиц со спином 1/ 2. В гл. 4 мы уже научились преобразовывать амплитуды для спина 1/ 2. Эти зна­ния можно применить к тому, чтобы получить преобразование для спина 1. Вот как это делается: имеется система (атом водо­рода с энергией + А) со спином 1. Пусть мы пропустили ее сквозь фильтр S Штерна — Герлаха так, что знаем теперь, что она находится в одном из базисных состояний по отношению к S, скажем в |+ S ). Какова амплитуда того, что она окажется в одном из базисных состояний, скажем |+ T ), по отношению к прибору Т? Если вы назовете систему координат прибора S системой х, у, z, то состояние |+ S > — это то, что недавно назы­валось состоянием |+ +>. Но представьте, что какой-то ваш приятель провел свою ось z вдоль оси Т. Он свои состояния будет относить к некоторой системе х ' , у ' , z'. Его состояния «вверх» и «вниз» для электрона и протона отличались бы от ваших. Его состояние «плюс — плюс», которое можно записать | +'+'>, отмечая «штрихованность» системы, есть состояние |+ Т > частицы со спином 1. А вас интересует <+ T |+ S >, что есть просто иной способ записи амплитуды <+'+' | + + >.

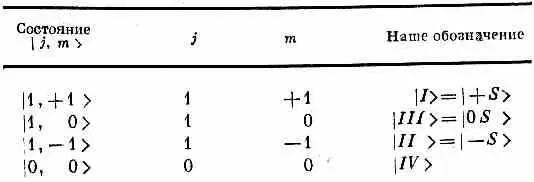
Амплитуду <+ '+' | + +> можно найти следующим обра­зом. В вашей системе спин электрона из состояния | + +> направлен вверх. Это означает, что у него есть некоторая ампли­туда <+'|+> eоказаться в системе вашего приятеля спином вверх и некоторая амплитуда <-' |+> еоказаться в этой системе спином вниз. Равным образом, протон в состоянии + + У имеет спин вверх в вашей системе и амплитуды <+'|+> ри <-'|+> pоказаться спином вверх или вниз в «штрихованной» системе. Поскольку мы говорим о двух раз­ных частицах, то амплитуда того, что обе частицы вместе в его системе окажутся спинами вверх, равна произведению амплитуд

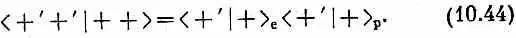
Мы поставили значки е и р под амплитудами <+'|+>, чтоб было ясно, что мы делаем. Но обе они — это просто ампли­туды преобразований для частицы со спином 1/ 2, так что на самом деле — это одни и те же числа. Фактически — это те же амплитуды, которые мы в гл. 4 называли <+ Т |+ S > > и которые мы привели в табл. 4.1 и 4.2.

Но теперь, однако, нам угрожает путаница в обозначениях. Надо уметь различать амплитуду <+ T |+ S ) для частицы со спином 1/ 2от того, что мы также назвали <+ T |+ S >, но для спина 1—между ними нет ничего общего! Надеюсь, вас не очень собьет с толку, если мы на время введем иные обозначения амплитуд для спина 1/ 2, Они приведены в табл. 10.4. Для состоя­ний частиц спина 1 мы по-прежнему будем прибегать к обозна­чениям | + S , | 0 S > и |- S >.

Таблица 10.4 · АМПЛИТУДЫ для СПИНА 1/ 2

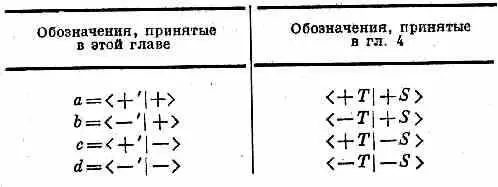
В наших новых обозначениях (10.44) просто превращается в

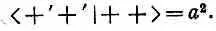
Это как раз амплитуда <+ T |+ S > для спина 1. Теперь давайте, например, предположим, что у вашего приятеля система коор­динат, т. е. «штрихованный» прибор Т, повернута вокруг вашей оси z на угол j; тогда из табл. 4.2 получается