Feynmann - Feynmann 8a

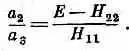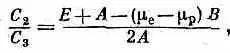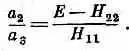
Отношение a 2 / a 3 — это, конечно, на сей раз C 2 / C 3 Вставляя аналогичные величины из (10.33), получаем

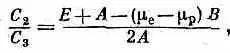
или

где вместо Е надо взять подходящую энергию (либо Е III , либо E IV ). Например, для состояния | III > имеем

Значит, при больших В у состояния | ///> С 2 > >С 3; состояние почти полностью становится состоянием | 2 >= |+ ->. Точно так же если в (10.39) подставить e iv , то получится, что (С 2/С 3) IV<<1; в сильных полях состояние | IV > обращается попросту в состояние |3> = |- +>. Вы видите, что коэффи­циенты в линейных комбинациях наших базисных состояний, составляющих стационарные состояния, сами зависят от В.

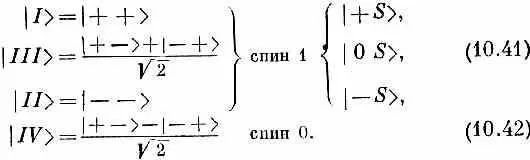
Состояние, которое мы име­нуем | III > , в очень слабых полях представляет собой смесь |+ -> и |- +> в про­порции 1:1, но в сильных полях целиком смещается к |+ ->. Точно так же и со­стояние | IV >, которое в сла­бых полях также является смесью |+ -> и |- +> в пропорции 1:1 (с обратным зна­ком), переходит в состояние | - + ), когда спины из-за силь­ного внешнего поля больше друг с другом не связаны.

Хотелось бы обратить ваше внимание, в частности, на то, что происходит в очень слабых магнитных полях. Имеется одна энергия ( -3 А ) , которая не изменяется при включении слабого магнитного поля. И имеется другая энергия ( + А ) , которая при включении слабого магнитного поля расщепляется на три различных уровня энергии. В слабых полях энергии с ростом В меняются так, как показано на фиг. 10.5. Допустим, что у нас есть каким-то образом отобранное множество атомов водорода, у которых у всех энергия равна - 3 А. Если пропу­стить их через прибор Штерна — Герлаха (с не очень сильными полями), то мы найдем, что они просто проходят целиком на­сквозь. (Поскольку их энергия не зависит от В, то, согласно принципу виртуальной работы, градиент магнитного поля не создает никакой силы, которая бы ощущалась ими.) Пусть, с другой стороны, мы бы отобрали группку атомов с энергией + А и пропустили их через прибор Штерна — Герлаха, скажем через прибор S. (Опять поля в приборе не должны быть столь сильными, чтобы разрушить внутренность атома; подразуме­вается, что поля малы настолько, что энергии можно считать линейно зависящими от В.) Мы бы получили три пучка. На состояния | I > и | II > действуют противоположные силы, их энергии меняются по В линейно с наклоном ±m, так что силы сходны с силами, действующими на диполь, у которого m z = ±m , а состояние | III > проходит насквозь. Мы опять возвращаемся к гл. 3. Атом водорода с энергией + А — это частица со спином 1. Это энергетическое состояние является «частицей», для которой j =1, и может быть описано (по отношению к некоторой системе осей в пространстве) в терминах базисных состояний |+ S >, | 0 S > и |- S > , которыми мы пользовались в гл. 3. С другой стороны, когда атом водорода имеет энергию -3 А, он является частицей со спином нуль. (Напоминаем, что все сказанное, строго говоря, справедливо лишь для бесконечно малых магнит­ных полей.) Итак, состояния водорода в нулевом магнитном поле можно сгруппировать следующим образом:

В гл. 35 (вып. 7) мы говорили, что у всякой частицы компо­ненты момента количества движения вдоль любой оси могут принимать только определенные значения, всегда отличаю­щиеся на h. Так, z-компонента момента количества движения J z может быть равна jh , (j-1) h, (j- 2) h ,..., (- j ) h , где j — спин частицы (который может быть целым или полу­целым). Обыкновенно пишут

J z =mh, (10.43)

где т стоит вместо любого из чисел j , j -1, j- 2, . . ., -j (в свое время мы не сказали об этом). Вы поэтому часто встре­тите в книжках нумерацию четырех основных состояний при помощи так называемых квантовых чисел j и m [часто именуе­мых «квантовым числом полного момента количества движения» ( j ) и «магнитным квантовым числом» ( m )]. Вместо наших сим­волов состояний | I >, | II > и т. д. многие часто пишут состоя­ния в виде | j , m > . Нашу табличку состояний для нулевого поля в (10.41) и (10.42) они бы изобразили в виде табл. 10.3. Здесь нет какой-либо новой физики, это просто вопрос обозначении.