Feynmann - Feynmann 8a

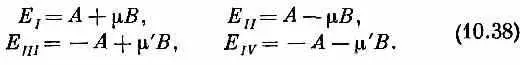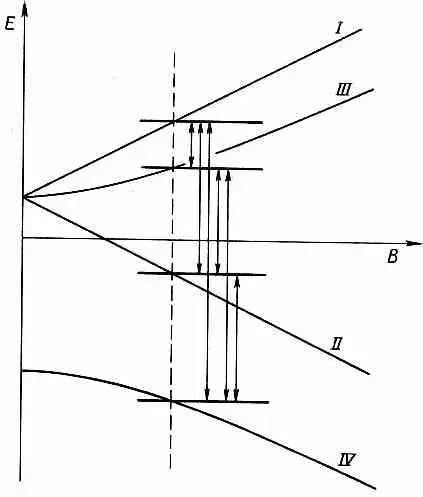
Фиг. 10.4. Переходы между уровнями энергии основного состояния водорода в некотором маг­нитном поле В.

Многие из этих переходов можно наблюдать с помощью техники молеку­лярных пучков Раби, которую мы описывали в гл. 35, § 3 (вып.7).

Что же является причиной переходов? Они возникают, если наряду с сильным постоянным полем B приложить малое возмущающее магнитное поле, которое меняется во времени. То же самое мы наблюдали и при действии переменного электрического поля на молекулу аммиака. Только здесь виновник переходов — это магнитное поле, действующее на магнитные моменты. Но теоретические выкладки те же самые, что и в случае аммиака. Проще всего они получаются, если взять возмущающее магнит­ное поле, вращающееся в плоскости ху, хотя то же будет от любого осциллирующего горизонтального поля. Если вы вста­вите это возмущающее поле в качестве добавочного члена в га­мильтониан, то получите решения, в которых амплитуды ме­няются во времени, как это было и с молекулой аммиака. Зна­чит, вы сможете легко и аккуратно рассчитать вероятность перехода из одного состояния в другое. И обнаружите, что все это согласуется с опытом.

§ 5 . Состояния в магнитном поле

Теперь займемся формой кривых на фиг. 10.3. Во-первых, если говорить о больших полях, то зависимость энергии от поля довольно интересна и легко объяснима. При достаточно боль­ших В (а именно при m B / A >>1) в формулах (10.37) можно пре­небречь единицей. Четверка энергий принимает вид

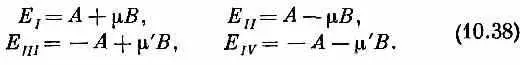
Это уравнения четырех прямых на фиг. 10.3. Эти формулы можно физически понять следующим образом. Природа стацио­нарных состояний в нулевом поле полностью определяется вза­имодействием двух магнитных моментов. Перемешивание ба­зисных состояний | + -> и | - +> в стационарных состояниях |III> и | IV > вызвано этим взаимодействием. Однако вряд ли можно ожидать, что каждая из наших частиц (и протон, и элек­трон) в сильных внешних полях будет испытывать влияние поля другой частицы; каждая будет действовать так, как если бы во внешнем поле находилась она одна. Тогда (как мы уже много раз видели) спин электрона окажется направленным вдоль внешнего магнитного поля (по нему или против него).

Пусть спин электрона направлен вверх, т. е. вдоль поля; энергия его будет -m e B . Протон при - этом может стоять по-разному. Если у него спин тоже направлен вверх, то его энергия -m p B . Их сумма равна -(m е+m р) B = m B . А это как раз и есть E I , и это очень приятно, потому что мы описываем состояние |+ +>=| I >. Есть еще небольшой дополнительный член А (теперь (m B >> A ), представляющий энергию взаимодействия протона и электрона, когда их спины параллельны. (Мы с са­мого начала считали А положительным, потому что так должно было быть по теории, о которой шла речь; то же получается и на опыте.) Но спин протона может быть направлен и вниз. Тогда его энергия во внешнем ноле обратится в +m Р B , а вместе с элек­троном их анергия будет -(m e-m р) В= m В. А энергия взаимо­действия обращается в - А. Их сумма даст энергию Е III , в (10.38). Так что состояние | III > в сильных полях становится состоянием |+ ->.

Пусть теперь спин электрона направлен вниз. Его энергия во внешнем ноле равна m e В. Если и протон смотрит вниз, то их общая энергия равна {m e+m p) В = - m В плюс энергия взаимо­действия А (спины-то теперь параллельны). Это приводит как раз к энергии Е II в (10.38) и соответствует состоянию |- ->=| II > , что очень мило. И наконец, если у электрона спин направлен вниз, а у протона — вверх, то мы получим энер­гию (m e-m p ) В - А (минус А потому, что спины противопо­ложны), т. е. E IV . А состояние отвечает |- +>.

«Погодите минутку,— вероятно, скажете вы.— «Состояния | Ill > и | IV > — это не состояния | + — > и | — + >; они яв­ляются их смесями». Верно, но перемешивание здесь едва замет­но. Действительно, при 5=0 они являются смесями, но мы пока не выясняли, что бывает при больших В. Когда мы для полу­чения энергии стационарных состояний пользовались анало­гией между (10.33) и формулами гл. 7, то заодно можно было оттуда взять и амплитуды. Они получатся из (7.23):