Feynmann - Feynmann 8a

Это значит, что к концу интервала времени Т состояние |y> будет представлять электрон, выстроенный в направлении, отличаю­щемся от первоначального только поворотом вокруг оси z на угол Dj =2 m B z T / h . Раз этот угол пропорционален Т, то можно говорить, что направление спина прецессирует вокруг оси z с угловой скоростью 2 m B z / h . Этот результат мы уже полу­чали раньше несколько раз, но не так полно и строго. Теперь мы получили полное и точное квантовомеханическое описание прецессии атомных магнитов.

Любопытно, что математические идеи, которые мы только что применили к электрону, вращающемуся в магнитном поле, применимы и для любой системы с двумя состояниями. Это озна­чает, что, проведя математическую аналогию с вращающимся электроном, можно при помощи чисто геометрических рассужде­ний решить любую задачу для двухуровневой системы. Сперва вы сдвигаете энергию так, чтобы ( H 11+ H 22) было равно нулю (так что H 11 = - H 22). И тогда любая задача о такой системе формально совпадет с задачей об электроне в магнитном поле. Вам нужно будет только отождествить — m B z с H 11, а -m (В х - iB y ) с H 12 . И неважно, какая физика там была перво­начально — молекула ли аммиака или что другое,— вы можете перевести ее на язык соответствующей задачи об электроне. Стало быть, если мы в состоянии решить в общем случае задачу об электроне, мы уже решили все задачи о двух состояниях.

А общее решение для электронов у нас есть! Пусть вначале электрон обладает определенным состоянием, в котором спин направлен вверх по некоторому направлению, а магнитное поле В — в какую-то другую сторону. Вращайте просто направление спина вокруг оси В с векторной угловой скоростью w( t ) , равной некоторой константе, умноженной на вектор В (а именно w=2m В/h). Если В меняется со временем, двигайте по-прежнему ось вращения так, чтобы она оставалась параллельной В, и изменяйте скорость вращения так, чтобы она все время была пропорциональна напряженности В (фиг. 8.11).

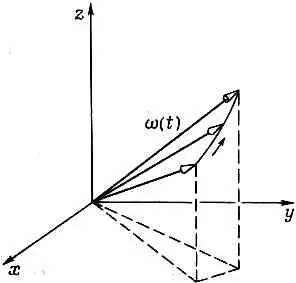
Фиг. 8.11. Направление спина электрона в изменяющемся магнит­ном поле В ( t ) прецессирует с част omo й w ( t ) вокруг оси, параллель­ной В.

Если все время это делать, вы остановитесь на какой-то конечной, ориентации спиновой оси, и амплитуды С 1 и С 2получатся просто как ее проекции [при помощи (8.30)] на вашу систему координат.

Вы видите, что задача эта чисто геометрическая: надо заме­тить, где закончились все ваши вращения. Хотя сразу видно, что для этого требуется, но эту геометрическую задачу (отыска­ние окончательного итога вращений с переменным вектором угловой скорости) нелегко в общем случае решить явно. Во вся­ком случае, мы в принципе видим общее решение любой задачи для двух состояний. В следующей главе мы глубже исследуем математическую технику обращения с частицами спина 1/ 2и, следовательно, обращения с системами, обладающими двумя состояниями, в общем случае.

* Мы принимаем энергию покоя m 0 c 2 за «нуль» энергии и считаем магнитный момент m электрона отрицательным числом, поскольку он направлен против спина.

* Сказанное нами может вас слегка ввести в заблуждение. Погло­щение ультрафиолетового света в принятой нами для бензола системе с двумя состояниями было бы очень слабым, потому что матричный элемент дипольного момента между двумя состояниями равен нулю. [Оба состояния электрически симметричны, и в нашей формуле (7.55) для ве­роятности перехода дипольный момент m равен нулю, и свет не погло­щается.] Если бы других состояний не было, существование верхнего со­стояния пришлось бы доказывать иными путями. Однако более полная теория бензола, которая исходит из большего числа базисных состояний (обладающих, скажем, смежными двойными связями), показывает, что истинные стационарные состояния бензола слегка искажены по сравне­нию с найденными нами. В результате все же возникает дипольный мо­мент, который и разрешает упомянутые в тексте переходы, приводящие к поглощению ультрафиолетового света.