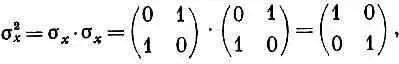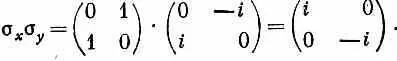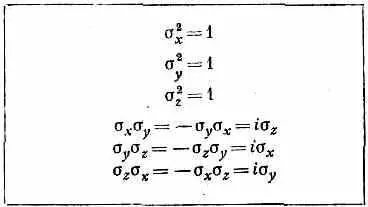Feynmann - Feynmann 8a

Вообще если мы «складываем» две матрицы А и В, то «сумма» С означает, что каждый ее элемент C ij дается формулой

C ij = A ij + B ij .

Каждый элемент С есть сумма элементов А и В, стоящих на тех же самых местах.

В гл. 3, § 6, мы уже сталкивались с представлением о матрич­ном «произведении». Та же идея полезна и при обращении с мат­рицами сигма. В общем случае «произведение» двух матриц A и В (в этом именно порядке) определяется как матрица С с элементами

Это — сумма произведений элементов, взятых попарно из i -й строчки А и k -ro столбца В. Если матрицы расписаны в виде таблиц, как на фиг. 9.1, то можно указать удобную «систему» получения элементов матрицы-произведения.

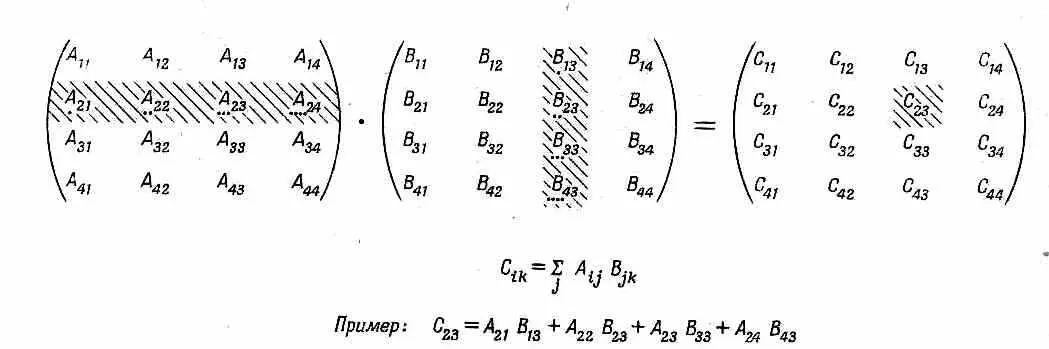
Фиг. 9.1. Перемножение двух матриц.

Скажем, вы вычисляете С 2 3 . Вы двигаете левым указательным пальцем по второй строчке А, а правым — вниз по третьему столбцу В, перемножаете каждую пару чисел и складываете пары по мере движения. Мы попытались изобразить это на рисунке.

Для матриц 2X2 это выглядит особенно просто. Например, если s х умножается на s x , то выходит

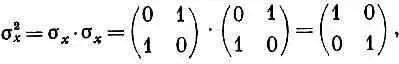
т. е. просто единичная матрица. Или, для примера, подсчита­ем еще

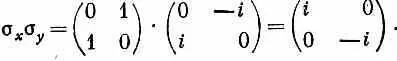
Взглянув на табл. 9.1, вы видите, что это просто матрица s x , умноженная на i . (Вспомните, что умножение матрицы на число означает умножение каждого элемента матрицы на число.) Попарные произведения сигм очень важны и выглядят они довольно забавно, так что мы их выписали в табл. 9.2. Вы сами можете подсчитать их, как мы сделали это с s 2 х и s х s y .

С матрицами о связан еще один очень интересный и важный момент. Можно, если угодно, представить себе, что три матрицы s х ., s y и s z подобны трем компонентам вектора; его иногда име­нуют «вектором сигма» и обозначают а. Это на самом деле «мат­ричный вектор», или «векторная матрица». Это три разные матрицы, связанные каждая со своей осью х, у или z . С их по­мощью гамильтониан системы можно записать в красивом виде, пригодном для любой системы координат:

Таблица 9.2 · ПРОИЗВЕДЕНИЯ СПИНОВЫХ МАТРИЦ

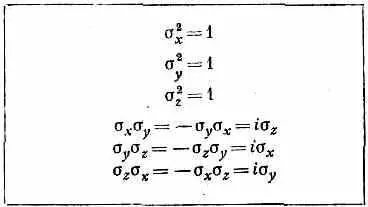
Хотя мы записали эти три матрицы в представлении, в кото­ром понятия «вверх» и «вниз» относятся к направлению z (так что s zвыглядит особенно просто), но можно представить себе, как будут они выглядеть в любом другом представлении. И хотя это требует немалых выкладок, можно все же показать, что они изменяются как компоненты вектора. (Мы, впрочем, пока не будем заботиться о том, чтобы доказать это. Проверьте сами, если хотите.) Вы можете пользоваться о в различных системах координат, как если бы это был вектор.

Вы помните, что гамильтониан Н связан в квантовой механике с энергией. Он действительно в точности совпадает с энергией в том простом случае, когда состояний только одно. Даже в системе с двумя состояниями, какой является спин электрона, если записать гамильтониан в виде (9.13), он очень напоминает классическую формулу энергии магнита с магнитным моментом m в магнитном поле В. Классически это выглядит так:

где m — свойство объекта, а В — внешнее поле. Можно вообра­зить себе, что (9.14) обращается в (9.13), если классическую энергию заменяют гамильтонианом, а классическое m — мат­рицей (ms. Тогда после такой чисто формальной замены результат можно будет интерпретировать как матричное уравнение. Иногда утверждают, что каждой величине в классической физике соответствует в квантовой механике матрица. На самом деле правильнее было бы говорить, что матрица Гамильтона соот­ветствует энергии и что у каждой величины, которая может быть определена через энергию, есть соответствующая матрица. Например, магнитный момент можно определить через энергию, сказав, что энергия во внешнем поле Весть — m· B. Это определяет вектор магнитного момента m . Затем мы смотрим на формулу для гамильтониана реального (квантового) объекта в магнитном поле и пытаемся угадать, какие матрицы соответ­ствуют тем или иным величинам в классической формуле. С помощью этого трюка иногда у некоторых классических вели­чин появляются их квантовые двойники.