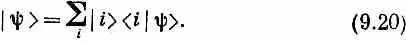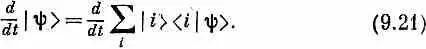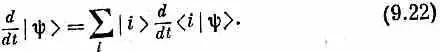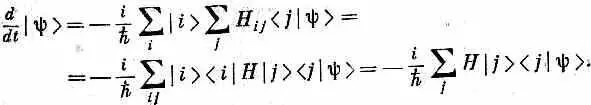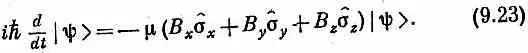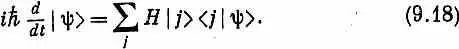
Или, сделав еще один шаг, убрать к тому же и j и написать

В гл. 6 мы указывали, что при такой записи Н в Н | j > или в Н |y> называется оператором. Отныне на операторы мы будем надевать маленькие шапочки (^), чтобы напоминать вам, что это оператор, а не число. Мы будем писать 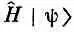
. Хотя оба уравнения (9.18) и (9.19) означают в точности то же самое, что и (9.15) или (9.17), мы можем думать о них совершенно иначе. Например, уравнение, (9.18) можно было бы описывать так: «Производная по времени от вектора состояния |y> равняется тому, что получается от действия оператора Гамильтона Н на каждое базисное состояние, умноженному на амплитуду < j |y> того, что y окажется в состоянии j , и просуммированному по всем j ». Или уравнение (9.19) можно описать так: «Производная по времени (умноженная на ih ) от состояния |y> равняется тому, что вы получите, если подействуете гамильтонианом Н на вектор состояния |y>». Это просто сокращенный способ выражения того, что содержится в (9.17), но, как вы потом убедитесь, он может оказаться очень удобным.
Если хотите, идею «абстрагирования» можно продвинуть еще на шаг. Уравнение (9.19) справедливо для всякого состояния |y>. Кроме того, левая сторона ihd / dt — это тоже оператор; его действие: «продифференцируй по t и умножь на ih ». Итак, (9.19) можно рассматривать как уравнение между операторами — операторное уравнение
Ih ( d / dt )= 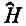
Оператор Гамильтона (с точностью до константы), действуя на любое состояние, приводит к тому же результату, что и d / dt . Помните, что это уравнение, как и (9.19), не есть утверждение о том, что оператор 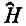 просто та же операция, что и d / dt . Эти уравнения — динамический закон природы (закон движения) для квантовой системы.
просто та же операция, что и d / dt . Эти уравнения — динамический закон природы (закон движения) для квантовой системы.
Только для того, чтобы попрактиковаться в этих представлениях, продемонстрируем вам другой вывод уравнения (9.18). Вы знаете, что любое состояние |y> можно записать через его проекции на какой-то базис [см. (6.8)]:
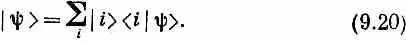
Как же меняется |y> во времени? Продифференцируем его:
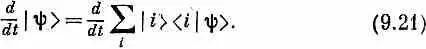
Но базисные состояния | i > во времени не меняются (по крайней мере у нас они всегда были определенными, закрепленными состояниями), и только амплитуды < i |y>—это числа, которые могут меняться. Иначе говоря, (9.21) прекращается в
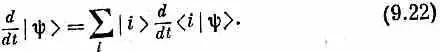
Но ведь d < i |y>/dt нам известно—это (9.16); получается, следовательно,
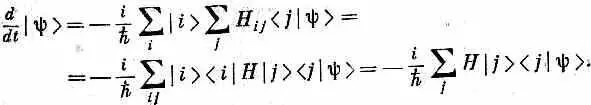
А это опять-таки уравнение (9.18).
Итак, на гамильтониан можно смотреть по-разному. Можно рассматривать совокупность коэффициентов H ij просто как компанию чисел, можно говорить об «амплитудах» < i | Н |j>, можно представлять себе «матрицу» H ij и можно считать его
«оператором» H ^ . Все это одно и то же.
Вернемся теперь к нашей системе с двумя состояниями. Если уж мы записываем гамильтониан через матрицы сигма (с подходящими численными множителями, такими, как В х и т. д.), то естественно рассматривать и s x ijкак амплитуду < i |s х | j >, или, для краткости, как оператор s^ л. Если применить эту идею оператора, то уравнение движения состояния |y> в магнитном поле можно написать в виде
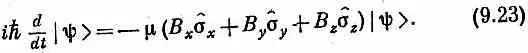
Желая «использовать» это уравнение, нам, естественно, приходится выражать |y> через базисные векторы (равносильно тому, что приходится находить компоненты пространственных векторов, когда задача доводится до числа). Так что обычно мы предпочитаем расписывать (9.23) в более раскрытом виде:
Читать дальше

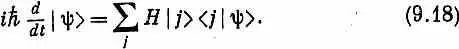

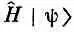
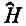
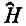 просто та же операция, что и d / dt . Эти уравнения — динамический закон природы (закон движения) для квантовой системы.
просто та же операция, что и d / dt . Эти уравнения — динамический закон природы (закон движения) для квантовой системы.