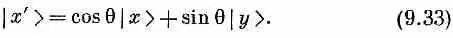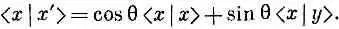Feynmann - Feynmann 8a

Итак, существуют два базисных состояния | x > и | y >, и их вполне хватает, чтобы описать всякий фотон.

К примеру, если у нас есть поляроид, ось которого распо­ложена так, чтобы пропускать свет, поляризованный в направ­лении, которое мы называем направлением х, и если мы напра­вили туда фотон, который, как нам известно, находится в состоя­нии | у >, то он поглотится поляроидом. Если послать туда фотон, который, как нам известно, находится в состоянии | х > , он и выйдет в состоянии | x >. Когда мы берем кусок кальцита (исландского пшата), который расщепляет пучок поляризован­ного света на | x >-пучок и | y >-пучок, то этот кусок кальцита полностью аналогичен прибору Штерна — Герлаха, расщеп­ляющему пучок атомов серебра на два состояния |+> и |->. Значит, все, что мы раньше делали с частицами и приборами Штерна — Герлаха, можно повторить со светом и кусками поляроида. А что можно сказать о свете, который отфильтрован куском поляроида, повернутым на угол 6? Другое ли это состоя­ние? Да, действительно, это другое состояние. Обозначим ось поляроида х ' , чтобы отличать ее от осей наших базисных состояний (фиг. 9.2).

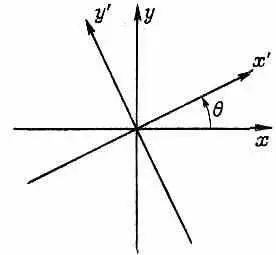
Фиг. 9.2. Оси координат, перпендику­лярные к вектору импульса фотона.

Выходящий наружу фотон будет в состоя­нии | х' >. Но всякое состояние может быть представлено в виде линейной комбинации базисных состояний, а формула для такой комбинации известна:

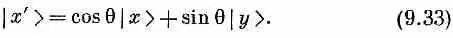
Иначе говоря, если фотон пройдет сквозь кусок поляроида, повернутого на угол q (по отношению к х), он все равно может быть разрешен на | x >- и | y >-пучки (например, куском каль­цита). Или, если угодно, вы можете в своем воображении просто разбить его на х- и y -компоненты. Любым путем вы получите амплитуду cosq быть в | х >-состоянии и амплитуду sinq быть в | y >-состоянии.

Теперь поставим такой вопрос: пусть фотон поляризован в направлении х' куском поляроида, повернутого на угол q,

и пусть он попадет в другой поляроид, повернутый на угол нуль (фиг. 9.3).

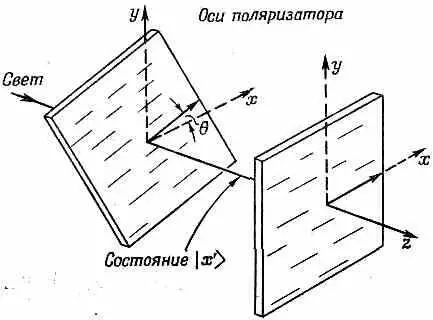
Фиг. 9.3. Две поляроидные пластины с углом q между плоскостями поляризации.

Что тогда произойдет? С какой вероятностью он прой­дет сквозь поляроид? Ответ: Пройдя первый поляроид, фотон наверняка оказывается в состоянии | х' > . Через второй поля­роид он протиснется лишь в том случае, если будет в состоянии | x > (и поглотится им, оказавшись в состоянии | у >). Значит, мы спрашиваем, с какой вероятностью фотон окажется в состоя­нии | x >? Эту вероятность мы получим из квадрата модуля амплитуды , амплитуды того, что фотон в состоянии | х ' > находится также и в состоянии | x >. Чему равно < x | x '>? Умножив (9.33) на < x |, получим

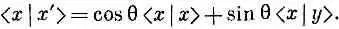
Но < x | y >=0; это следует из физики, так должно быть, если | х > и | у > суть базисные состояния, а < x | x >=l. И мы полу­чаем

< x | x '>=cosq,

а вероятность равна cos 2q. Например, если первый поляроид поставлен под углом 30°, то 3/ 4времени фотон будет проходить через него, a 1/ 4 времени будет нагревать поляроид, поглощаясь внутри него.

Посмотрим теперь, что в такой же ситуации происходит с точки зрения классической физики. Там мы имели бы пучок света, электрическое поле которого меняется тем или иным обра­зом,— скажем «неполяризованный» пучок. После того как он прошел бы через первый поляроид, электрическое поле величи­ны x начало бы колебаться в направлении х ' ; мы бы начертили его в виде колеблющегося вектора с пиковым значением x 0 на диаграмме фиг, 9.4.

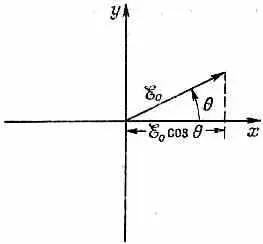
Фиг. 9.4. Классическая картина электрического вектора x .

Если бы затем свет достиг второго поля­роида, то черен него прошла бы только x -компонента x 0cosq электрического поля. Интенсивность была бы пропорциональна квадрату поля, т. е. x2cos 2q. Значит, проходящая сквозь последний поляроид энергия была бы в cos 2q слабее энергии, поступающей в него.