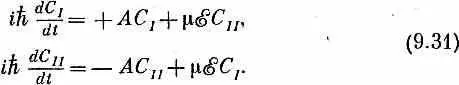Feynmann - Feynmann 8a

Только что описанное решение достаточно общо для того. чтобы справиться с любой системой с двумя состояниями. Возь­мем наш пример с молекулой аммиака, на которую действует электрическое поле. Если система описывается на языке состоя­ний | I > и | II >, то уравнения выглядят так:

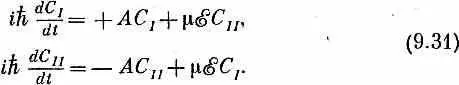
Вы скажете: «Нет, там, я помню, стояло еще E 0». Неважно, мы просто сдвинули начало отсчета энергий, чтобы Е 0 стало равно нулю. (Это всегда можно сделать, изменив обе амплитуды в одно и то же число раз — в e iE 0 T / h ; так можно избавить­ся от любой постоянной добавки к энергии.) Одинаковые урав­нения обладают одинаковыми решениями, поэтому не стоит решать их вторично. Если взглянуть на эти уравнения и на (9.1), то их можно отождествить между собой следующим образом. Состояние |+> обозначим | I >, состояние |-> обозначим | Н > . Это вовсе не значит, что мы выстраиваем аммиак в про­странстве в одну линию или что |+> и |-> как-то связаны с осью z. Это все делается чисто искусственно. Имеется искусст­венное пространство, которое можно было бы назвать, например, «модельным пространством молекулы аммиака» или еще как-нибудь иначе. Это просто трехмерная «диаграмма», и направле­ние «вверх» означает пребывание молекулы в состоянии | I >, а направление «вниз» по фальшивой оси z означает пребывание молекулы в состоянии | II >. Тогда уравнения отождествляются следующим образом.

Прежде всего вы видите, что гамильтониан может быть записан через матрицы сигма:

Если сравнить это с (9.1), то m B z будет соответствовать - А, а m В х будет соответствовать -mx . В нашем «модельном» про­странстве возникает, стало быть, постоянное поле В, направ­ленное по оси z . Если есть, кроме этого, электрическое поле x, меняющееся со временем, то у поля В появится и пропорцио­нально меняющаяся x -компонента. Таким образом, поведение электрона в магнитном поле с постоянной составляющей в на­правлении z и колеблющейся составляющей в направлении х математически во всем подобно и точно соответствует поведе­нию молекулы аммиака в осциллирующем электрическом поле, К сожалению, у нас нет времени входить глубже в детали этого соответствия или разбираться в каких-либо технических дета­лях. Мы только хотели подчеркнуть, что можно сделать так, чтобы все системы с двумя состояниями были аналогичны объек­ту со спином 1/ 2 , прецессирующему в магнитном поле.

§ 4. Состояния поляризации фотона

Есть множество других интересных для изучения систем с двумя состояниями, и первая, о которой мы бы хотели пого­ворить,— это фотон. Чтобы описать фотон, нужно сначала задать вектор его импульса. У свободного фотона импульс определяет и частоту, так что указывать особо частоту не придется. Но еще остается одно свойство, именуемое поляризацией. Представьте себе фотон, приходящий к вам с определенной монохроматиче­ской частотой (которую во всем нашем обсуждении мы будем считать постоянной, так что можно не говорить о множестве состояний импульса).Тогда существуют два направления поля­ризации. По классической теории свет обладает, например, либо горизонтально колеблющимся электрическим полем, либо вертикально колеблющимся электрическим полем; этот свет двух сортов называют x -поляризованным и y -поляризованным светом. У света может быть и какое-то иное направление поляризации, его можно создать суперпозицией полей в направ­лении x и в направлении у. Или, взяв х- и y -компоненты со сдви­гом фаз в 90°, получить вращающееся электрическое поле — свет будет поляризован эллиптически. [Это краткое напомина­ние классической теории поляризованного света, которую мы изучали в гл. 33 (вып. 3).]

Пусть теперь у нас есть одиночный фотон, всего один. Уже нет электрического поля, которое можно было бы рассматривать прежним способом. Один-единственный фотон и ничего больше. по он тоже должен обладать аналогом классического явления поляризации. Значит, должны существовать по крайней мере два разных сорта фотонов. Сперва могло бы показаться, что их должно быть бесконечное множество, ведь, как бы то ни было, электрический вектор может быть направлен в любую сторону. Однако поляризацию фотона можно описать как систему с двумя состояниями. Фотон может быть либо в состоянии |х > , либо |в состоянии | у > . Под | х > подразумевается состояние поляризации каждого из фотонов в пучке света, который классически x -поляризован. А | у > означает состояние поляризации каждого из фотонов в y -поляризованном пучке. Эти | х > и |у > вы можете выбрать в качестве базисных состояний фотона с данным [направленным на вас импульсом—импульсом в направлении z .