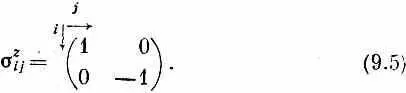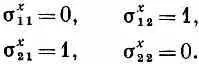* Мы немного упрощаем дело. Первоначально химики думали, что должны существовать четыре формы дибромбензола: две формы с атомами брома при соседних атомах углерода (орто-дибромбензол), третья форма с атомами брома при атомах углерода, идущих через один (.мета-дибромбензол), и четвертая форма с атомами брома, стоящими друг против друга (пара-дибромбензол). Однако отыскали они только три формы — существует лишь одна форма орто-молекулы.
* До тех пор, пока нет сильных магнитных полей, это предположение вполне удовлетворительно. Влияние магнитных полей на электрон мы обсудим в этой же главе позже, а очень слабые спиновые эффекты в атоме водорода — в гл. 10.
Глава 9
ЕЩЕ СИСТЕМЫ С ДВУМЯ
состояниями
§ 1. Спиновые матрицы Паули
§ 2.Спиновые матрицы как операторы
§ З. Решение уравнений для двух состояний
§ 4. Состояния поляризации фотона
§ 5. Нейтральный K-мезон *
§ 6. Обобщение на системы с N состояниями
Повторить: гл. 33 (вып. 3) «Поляризация»
§ 1 . Спиновые матрицы. Паули
Продолжаем обсуждение свойств двухуровневых систем. В конце предыдущей главы мы говорили о частице со спином l/ 2 в магнитном поле. Мы описывали спиновое состояние, задавая амплитуду С 1 того, что z-компонента спинового момента количества движения равна +h/2, и амплитуду С 2того, что она равна - h /2. В предыдущих главах мы эти базисные состояния обозначали |+> и |->. Прибегнем опять к этим обозначениям, хотя, когда это будет удобнее, мы будем менять их на | 1 > и | 2 >. Мы видели в последней главе, что когда частица со спином 1/ 2и с магнитным моментом m, находится в магнитном поле В =(В x , В y , B z ), то амплитуды С + ( = C 1) и С - (= С 2) связаны следующими дифференциальными уравнениями:
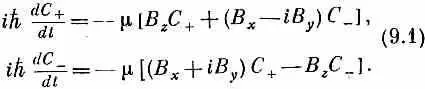
Иначе говоря, матрица-гамильтониан H ij имеет вид
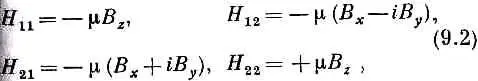
конечно, уравнения (9.1) совпадают с
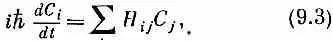
где i и j принимают значения + и - (или 1 и 2).
Эта система с двумя состояниями — спин электрона — настолько важна, что очень полезно было бы найти для ее описания способ поаккуратнее и поизящнее. Мы сейчас сделаем небольшое математическое отступление, чтобы показать вам, как обычно пишутся уравнения системы с двумя состояниями. Это делается так: во-первых, заметьте, что каждый член гамильтониана пропорционален m, и некоторой компоненте В; поэтому (чисто формально) можно написать
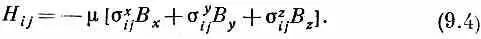
Здесь нет какой-либо новой физики; эти уравнения просто означают, что коэффициенты 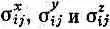 — их всего 4X3=12 — могут быть представлены так, что (9.4) совпадет с (9.2).
— их всего 4X3=12 — могут быть представлены так, что (9.4) совпадет с (9.2).
Посмотрим, почему это так. Начнем с B z . Раз В zвстречается только в H 11и H 22, то все будет в порядке, если взять

Мы часто пишем матрицу H ij в виде таблички такого рода:
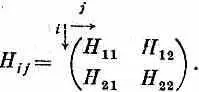
Для гамильтониана частицы со спином 1/ 2в магнитном поле В—это все равно что 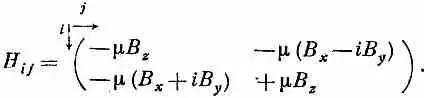
Точно так же и коэффициенты 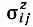 можно записать в виде матрицы
можно записать в виде матрицы
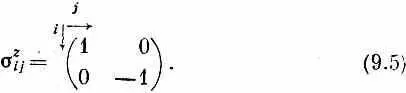
Расписывая коэффициенты при В х , получаем, что элементы матрицы s х должны иметь вид
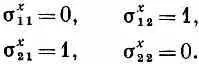
Читать дальше

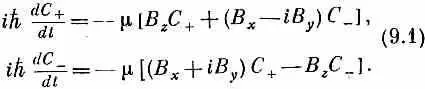
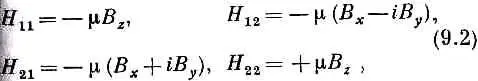
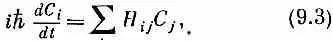
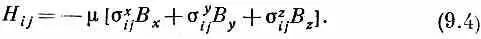
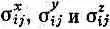 — их всего 4X3=12 — могут быть представлены так, что (9.4) совпадет с (9.2).
— их всего 4X3=12 — могут быть представлены так, что (9.4) совпадет с (9.2).
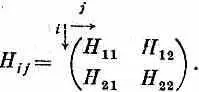
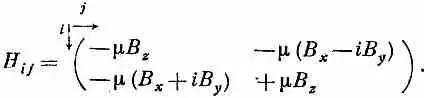
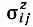 можно записать в виде матрицы
можно записать в виде матрицы