B z = Bcos q , В х =В sinqсоsj, В у =В sinqsinj.
Тогда мы имеем
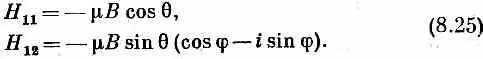
Кстати, скобка во втором уравнении есть просто 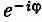 , так что проще писать
, так что проще писать
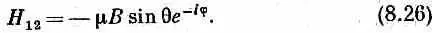
Подставляя эти матричные элементы в (8.24) и сокращая на -m B , находим

Зная это отношение и зная условие нормировки, можно найти и а 1 , и а 2. Сделать это нетрудно, но мы сократим путь, прибегнув к одному трюку. Известно, что
1-cosq=2sin 2(q/2) и sinq=2sin(q/2)cos(q/2). Значит, (8.27) совпадает с

Один из ответов, следовательно, таков:
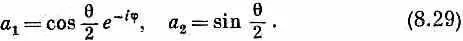
Он удовлетворяет и уравнению (8.28), и условию
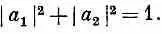
Вы знаете, что умножение a 1и а 2на произвольный фазовый множитель ничего не меняет. Обычно формуле (8.29) предпочитают более симметричную запись, умножая на e'f' 2. Принято писать так:
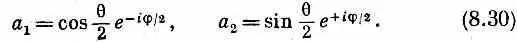
Это и есть ответ на наш вопрос. Числа а 1 и а 2— это амплитуды того, что электрон будет замечен спином вверх или вниз (по отношению к оси z ), если известно, что его спин направлен вдоль оси (q,j). [Амплитуды C 1 и С 2 равны просто a 1и a 2, умноженным на 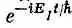
Заметьте теперь занятную вещь. Напряженность В магнитного поля нигде в (8.30) не появляется. Тот же результат разумеется, получится в пределе, если поле В устремить к нулю Это означает, что мы дали общий ответ на вопрос, как представлять частицу, спин которой направлен вдоль произвольной оси. Амплитуды (8.30) — это проекционные амплитуды для частиц со спином 1/ 2, подобные проекционным амплитудам для частиц со спином 1, приведенным в гл. 3 [уравнения (3.38)]. Теперь мы сможем находить для фильтрованных пучков частиц со спином 1/ 2амплитуды проникновения через тот или иной фильтр Штерна — Герлаха.
Пусть |+z> представляет состояние со спином, направленным по оси z вверх, а |-z> — состояние со спином вниз. Если | +z'> представляет состояние со спином, направленным вверх по оси z ' , образующей с осью z углы q и j, то в обозначениях гл. 3 мы имеем
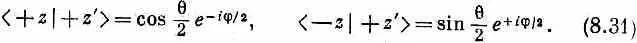
Эти результаты эквивалентны тому, что мы нашли из чисто геометрических соображений в гл. 4 [уравнение (4.36)]. (Если вы в свое время решили пропустить гл. 4, то вот перед вами один из ее существенных результатов.)
Напоследок вернемся еще раз к тому примеру, о котором уже не раз говорилось. Рассмотрим такую задачу. Сперва имеется электрон с определенным образом направленным спином, затем на 25 минут включается магнитное поле в направлении z , а затем выключается. Каким окажется конечное состояние? Опять представим состояние в виде линейной комбинации |y>=| 1 > C 1+| 2 > С 2 , Но в нашей задаче состояния с определенной энергией являются одновременно нашими базисными состояниями | 1 > и | 2 > , Значит, С 1 и С 2меняются только по фазе. Мы знаем, что
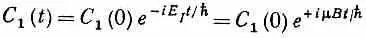
и
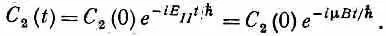
Мы сказали, что вначале у спина электрона было определенное направление. Это означает, что вначале С 1 и С 2 были двумя числами, определяемыми формулами (8.30). Переждав Т секунд, новые С 1и С 2мы получим из прежних умножением соответственно на 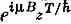 и
и 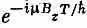 . Что это будут за состояния? Узнать это легко, ведь это все равно, что изменить угол j, вычтя из него 2 m B z T / h , и не трогать угол q.
. Что это будут за состояния? Узнать это легко, ведь это все равно, что изменить угол j, вычтя из него 2 m B z T / h , и не трогать угол q.
Читать дальше

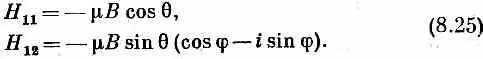
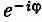 , так что проще писать
, так что проще писать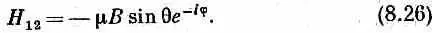


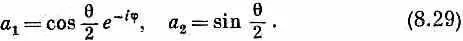
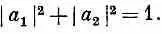
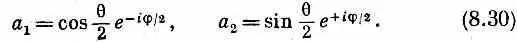
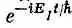
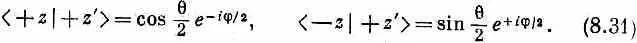
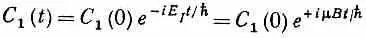
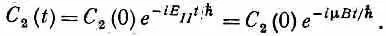
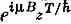 и
и 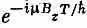 . Что это будут за состояния? Узнать это легко, ведь это все равно, что изменить угол j, вычтя из него 2 m B z T / h , и не трогать угол q.
. Что это будут за состояния? Узнать это легко, ведь это все равно, что изменить угол j, вычтя из него 2 m B z T / h , и не трогать угол q.










