Feynmann - Feynmann 8

Теперь мы вправе сказать: «Состояние y — это то, что полу­чается, если начать с j и пройти сквозь аппарат A ».

Еще один, последний пример полезных уловок. Начинаем опять с (6.17). Раз это уравнение соблюдается при любых c и j, то их обоих можно сократить! Получаем

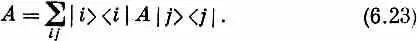
Что это значит? Только то, что получится, если вернуть на свои места j и c. В таком виде это уравнение «недокончено» и неполно. Если умножить его «справа» на |j>, то оно превра­щается в

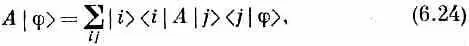
а это снова то же уравнение (6.22). В самом деле, мы бы могли просто убрать из (6.22) все j и написать

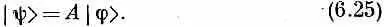
Символ А — это не амплитуда и не вектор; это вещь осо­бого рода, именуемая оператором. Он — нечто, что «опериру­ет» над состоянием, чтобы создать новое состояние; уравнение (6.25) говорит, что |y)> — это то, что получается, если А дей­ствует на |j>. Это уравнение тоже нужно считать недокончен­ным, открытым, пока слева оно не умножится на какое-то «брэ», скажем на

Оператор А, разумеется, полностью описывается тем, что за дается матрица амплитуд < i | A | j >; ее также пишут в виде А ij — через любую совокупность базисных векторов.

Все эти математические обозначения на самом деле ничего нового не вносят. Единственный резон, почему мы их ввели,— мы хотели показать, как пишутся обрывки уравнений, потому что во многих книжках вы встретите уравнения, написанные в неполном виде, и нет причин вам пугаться, увидев их. Если вы захотите, вы всегда сможете дописать те части, которых не хватает, и получить уравнение, связывающее числа. Оно будет выглядеть более привычно.

Кроме того, как вы увидите, обозначения «брэ» и «кет» очень удобны. Прежде всего мы теперь сможем указывать со­стояния, задавая их вектор состояния. Когда мы захотим вести речь о состоянии с определенным импульсом р, то скажем: «состояние

| р>». Или будем говорить о некотором произволь­ном состоянии |y>. Для единообразия мы всегда, говоря о состоянии, будем употреблять «кет» и писать |y>. (Конечно, этот выбор совершенно произволен; в равной мере мы могли бы остановиться и на «брэ»

§ 3. Каковы базисные состояния мира?

Мы обнаружили, что всякое состояние в мире может быть представлено в виде суперпозиции (линейной комбинации с подходящими коэффициентами) базисных состояний. Вы вправе спросить, во-первых: каких именно базисных состояний? Что ж, возможностей здесь немало. Можно, например, взять проек­цию спина на направление z или на некоторое другое направ­ление. Имеется очень-очень много различных представлений — аналогов различных систем координат, которые можно при­менять для представления обычных векторов. Затем можно спросить: с какими коэффициентами их брать? А это уж за­висит от физических обстоятельств. Различные совокупности коэффициентов отвечают разным физическим условиям. Здесь важно знать одну вещь — «пространство», в котором вы ра­ботаете, иными словами, знать, что эти базисные состояния означают физически. Так что первое, что вы, вообще говоря, должны знать,— это на что похожи базисные состояния. Тогда вам станет понятно, как описывать положение вещей на языке этих базисных состояний.

Мы хотели бы чуть-чуть заглянуть вперед и немножко по­говорить о том, каким скорей всего окажется общее квантовомеханическое описание природы — во всяком случае, каким оно будет, судя по нынешним физическим представлениям. Первым делом надо решиться на тот или другой выбор пред­ставления базисных состояний (всегда ведь возможны различ­ные представления). Например, для частицы со спином 1/ 2можно использовать плюс- и минус-состояния относительно оси z . В оси z нет ничего особенного — можете выбрать любую ось, какую вам захочется. Но для единообразия мы всегда будем брать ось z . Начнем со случая одного электрона. Наряду с двумя возможностями для спина (вверх и вниз по оси z) электрон имеет еще импульс. Мы выбираем совокупность ба­зисных состояний, по одному на каждое значение импульса. А что если у электрона нет определенного импульса? Ничего страшного: мы ведь говорим только, каковы базисные состоя­ния. Если у электрона не будет определенного импульса, то у него какая-то амплитуда будет иметь один импульс, а какая-то — другой и т. д. А если он вертится не обязательно вверх спином, то у него есть какая-то амплитуда вертеться при этом импульсе спином вверх, а какая-то — вниз и т. д. Для пол­ного описания электрона, насколько нам сейчас известно, требуется только, чтобы базисные состояния описывались импульсом и спином. Значит, одна из приемлемых совокуп­ностей базисных состояний | i > для отдельного электрона ука­зывает различные значения импульса и еще направление, куда смотрит спин,— вверх или вниз. Различные смеси амплитуд, т. е. различные сочетания чисел С, описывают различные об­стоятельства. Что делает тот или иной электрон, описывается тем, что сообщается, с какой амплитудой у него спин может быть вверх, а с какой — вниз, и при этом импульс будет равен тому или иному числу, и так для всех мыслимых импульсов. Вы теперь видите, что требуется для полного квантовомеханического описания отдельного электрона.