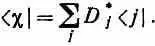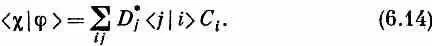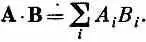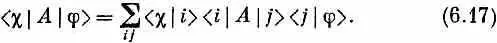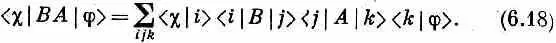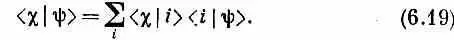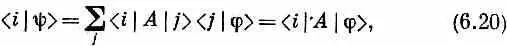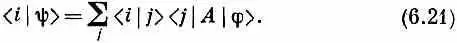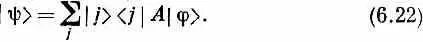Вспоминая, что i >=< i |c>*, можно записать это в виде

А теперь интересно вот что: чтобы обратно получить , можно просто перемножить (6.13) и (6.10). Только, делая это, надо быть внимательным к индексам суммирования, потому что они в разных уравнениях разные. Перепишем сперва (6.13):
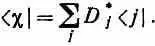
Это ничего не меняет. Объединяя с (6.10), получаем
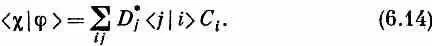
Вспомните, однако, что i >=d ij, так что в сумме останутся только члены с j = i . Выйдет

где, как вы помните, d * i =< i |c>*=i >, а C i =. Опять мы являемся свидетелями тесной аналогии со скалярным произведением
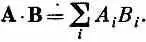
Единственная разница — что D i нужно комплексно сопрягать. Значит, (6.15) утверждает, что если разложить векторы состояний по базисным векторам < i | или | i ), то амплитуда перехода из j в c дается своего рода скалярным произведением (6.15). А это просто (6.1), записанное в других символах. Мы ходим по кругу, привыкая к новым символам.
Может быть, стоит подчеркнуть, что в то время, как пространственные трехмерные векторы выражаются через три ортогональных единичных вектора, базисные векторы | i > квантовомеханических состояний должны пробегать всю совокупность, отвечающую данной задаче. В зависимости от положения вещей в нее может входить два или три, пять или бесконечно много базисных состояний.
Мы говорили также о том, что происходит, когда частицы проходят через прибор. Если мы выпустим частицы в определенном состоянии j, затем проведем их через прибор, а после проделаем измерение, чтобы посмотреть, находятся ли они в состоянии c, то результат будет описываться амплитудой

Такой символ не имеет близкого аналога в векторной алгебре. (Он ближе к тензорной алгебре, но эта аналогия не так уж полезна.) Мы видели в гл. 3 [формула (3.32)], что (6.16) можно переписать так:
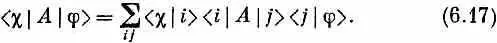
Это пример двукратного применения основного правила (6.9).
Мы обнаружили также, что если вслед за прибором А по ставить другой прибор 5, то можно написать
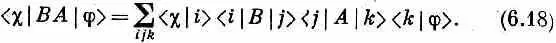
Это опять-таки следует прямо из предложенного Дираком метода записи уравнения (6,9). Вспомните, что между В и A всегда можно поставить черту (|), которая ведет себя совсем как множитель единица.
Кстати говоря, об уравнении (6.17) можно рассуждать и иначе. Предположим, что мы рассуждаем о частице, попадающей в прибор А в состоянии j и выходящей из него в состоянии y. Мы можем задать себе такой вопрос: можно ли найти такое состояние y, чтобы амплитуда перехода от y к c тождественно совпадала с амплитудой A |j>? Ответ гласит да. Мы хотим, чтобы (6.17) заменилось уравнением
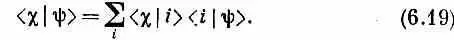
Конечно, этого можно достичь, если взять
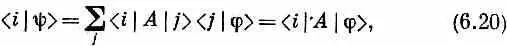
что и определяет собой y. «Но оно не определяет собой y,— скажете вы,— оно определяет только < i |y>». Однако все же определяет y; ведь если у вас есть все коэффициенты, связывающие y с базисными состояниями i , то y определяется однозначно. И действительно, можно поупражняться с нашими обозначениями и записать (6.20) в виде
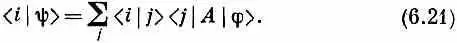
А раз это уравнение справедливо при всех г, то можно просто писать
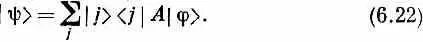
Читать дальше