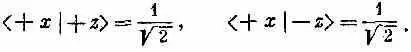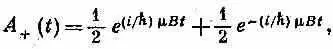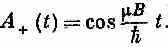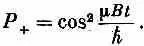Пусть |y(t)> представляет состояние мюона. Когда он входит в блок А, его состояние есть |y (0)>, а мы. хотим знать |y (t)> в более позднее время t. Если два базисных состояния обозначить (+z) и (-z), то нам известны амплитуды <+z|y (0)> и <-z|y (0)> — они известны потому, что мы знаем, что |y (0)> представляет собой состояние со спином в направлении (+ x ). Из предыдущей главы следует, что эти амплитуды равны
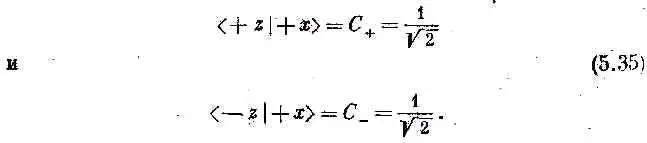
Они оказываются одинаковыми. Раз они относятся к положению при t=0, обозначим их С +(0) и С -(0).
Далее, мы знаем, что из этих двух амплитуд получится со временем. Из (5.34) следует
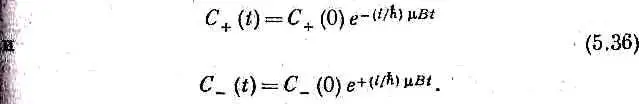
Но если нам известны C + ( t ) и C - ( t ), то у нас есть все, чтобы знать условия в момент t . Надо преодолеть только еще одно затруднение: нужна-то нам вероятность того, что спин (в момент t ) окажется направленным по + х. Но наши общие правила учитывают и эту задачу. Мы пишем, что амплитуда пребывания в состоянии ( + x ) в момент t [обозначим ее A + ( t )] есть
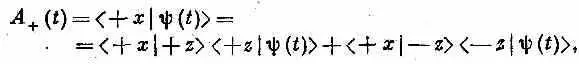
или
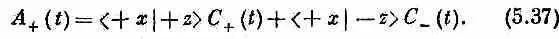
Опять пользуясь результатом последней главы (или лучше равенством
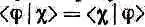 * из гл. 3), мы пишем
* из гл. 3), мы пишем
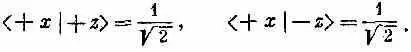
Итак, в (5.37) все известно. Мы получаем
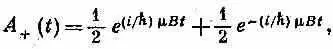
или
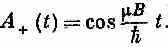
Поразительно простой результат! Заметьте: ответ согласуется с тем, что ожидалось при t = 0 . Мы получаем А + (0) = 1 , и это вполне правильно, потому что сперва и было предположено, что при t =0 мюон был в состоянии (+ x ).
Вероятность Р + того, что мюон окажется в состоянии ( + х) в момент t , есть (А +) 2, т. е.
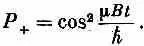
Вероятность колеблется от нуля до единицы, как показано на фиг. 5.10.
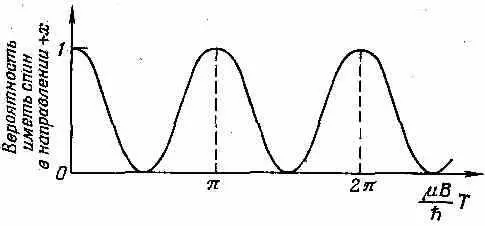
Фиг. 5.10. Временная зависимость в epo ятности того. что частица со спином 1 / 2 окажется в состоянии (+) по отношению оси х.
Заметьте, что вероятность возвращается к единице при m Bt / h = p (а не при 2p). Из-за того что косинус возведен в квадрат, вероятность повторяется с частотой 2 m В/ h .
Итак, мы обнаружили, что шанс поймать в электронном счетчике, показанном на фиг. 5.9, распадный электрон периодически меняется с величиной интервала времени, в течение которого мюон сидел в магнитном поле. Частота зависит от магнитного момента (Л. Именно таким образом и был на самом деле измерен магнитный момент мюона.
Тем же методом, конечно, можно воспользоваться, чтобы ответить на другие вопросы, касающиеся распада мюона. Например, как зависит от времени t шанс заметить распадный электрон в направлении у, под 90° к направлению х, но по-прежнему под прямым углом к полю? Если вы решите эту задачу, то увидите, что вероятность оказаться в состоянии ( + у) меняется как cos 2 {(m Bt / h )-(p/4)}; она колеблется с тем же периодом, но достигает максимума на четверть цикла позже, когда mВt/h=p/4. На самом-то деле происходит вот что: с течением времени мюон проходит через последовательность состояний, отвечающих полной поляризации в направлении, которое непрерывно вращается вокруг оси z . Это можно описать, говоря, что спин прецессирует с частотой

Вам должно становиться понятно, в какую форму выливается квантовомеханическое описание, когда мы описываем поведение чего-либо во времени.
Читать дальше

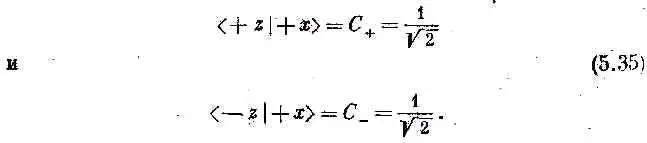
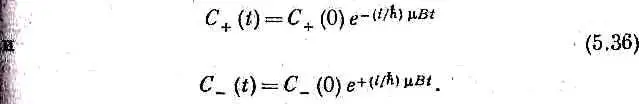
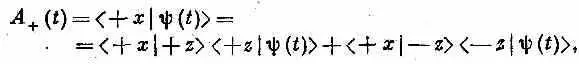
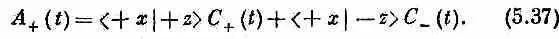
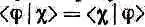 * из гл. 3), мы пишем
* из гл. 3), мы пишем