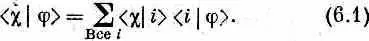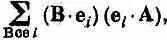Feynmann - Feynmann 8

* Если вы пропустили гл. 4, то можете пока просто считать (5.35) невыведенным правилом. Позже, в гл. 8, мы разберем прецессию спина подробнее, будут получены и эти амплитуды.

* Мы предполагаем, что фазы обязаны иметь одно и то же значение в соответствующих точках в двух системах координат. Впрочем, это весьма тонкое место, поскольку в квантовой механике фаза в значитель­ной степени произвольна. Чтобы до конца оправдать это предположение, нужны более детальные рассуждения, учитывающие интерференцию двух или нескольких амплитуд.

Г лава 6

ГАМИЛЬТОНОВА МАТРИЦА

§ 1. Амплитуды и векторы

§ 2. Разложение век­торов состояний

§ 3. Каковы базисные состояния мира?

§ 4. Как состояния меняются во времени

§ 5. Гамильтонова матрица

§ б. Молекула аммиака

Пов торить: гл. 49) (вып. 4) «Собст­венные колеба­ния»

§ 1. Амплитуды и векторы

Прежде чем приступить к основной теме этой главы, мы хотели бы изложить несколько математических идей, которые часто встреча­ются в книгах по квантовой механике. Знание их облегчит вам чтение других книг или статей по этому предмету. Первая идея — это тесное математическое подобие между уравнениями квантовой механики и формулами для скаляр­ного произведения двух векторов. Вы помните, что если c и j — два состояния, то амплитуда начать в j и кончить в c может быть записана в виде суммы (по полной совокупности базис­ных состояний) амплитуд перехода из j в одно из базисных состояний и затем из этого базис­ного состояния уже в c:

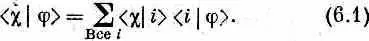
Мы объясняли это при помощи прибора Штер­на — Герлаха, но сейчас напоминаем вам, что в этих приборах нет нужды. Уравнение (6.1) — это математический закон, который верен всег­да, все равно, есть ли у нас фильтровальное оборудование или нет; вообще совсем не обя­зательно воображать наличие какого-то при­бора. Можно рассматривать это просто как формулу для амплитуды .

Сопоставим (6.1) с формулой для скалярного произведения двух векторов В и А. Если В и А — обычные трехмерные векторы, то ска­лярное произведение можно написать так:

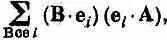
считая, что символ е iобозначает любой из трех единичных векторов в направлениях х.у и z. Тогда B · e 1 — это то, что обычно называют В х , а В · е 2 — то, что обычно называют B y , и т, д. Значит, (6.2) эквивалентно

В х А х +В у А у +В г А г ,

а это и есть скалярное произведение В · А.

Сравнение (6.1) с (6.2) обнаруживает следующую аналогию. Состояния c и j соответствуют двум векторам А и В. Базис­ные состояния i отвечают специальным векторам е i, к которым мы относим все прочие векторы. Любой вектор может быть представлен как линейная комбинация трех «базисных векто­ров» е i. Далее, если вам известны коэффициенты при каждом «базисном векторе» в этой комбинации, т. е. три его компонен­ты, то вы знаете о векторе все. Точно так же любое квантовомеханическое состояние может быть полностью описано ампли­тудами < i |j> перехода в базисные состояния, и если эти коэф­фициенты вам известны, то вы знаете все, что можно знать о состоянии. Из-за этой тесной аналогии то, что мы назвали «состоянием», часто именуют «вектором состояния».

Раз базисные векторы е i перпендикулярны друг другу, то существует соотношение

Это соответствует соотношению (3.25) между базисными со­стояниями i

Теперь вы понимаете, почему говорят, что базисные состоя­ния i все «ортогональны друг другу».

Между (6.1) и скалярным произведением есть одно мини­мальное различие. У нас