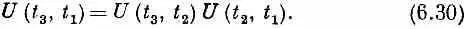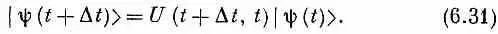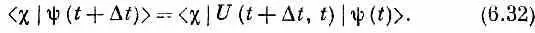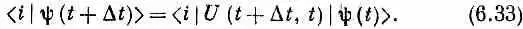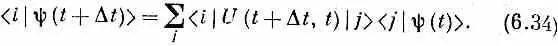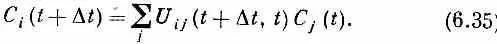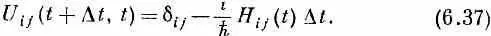Feynmann - Feynmann 8

Рассмотрим матрицу U для задержки от t 1 до t 3 , где t 3больше t 2 . Иными словами, возьмем три последовательных момента: t 1меньше t 2, t 2меньше t 3 . Тогда мы утверждаем, что матрица, которая тянется от t 1 до t 3 , получается перемноже­нием подряд всего того, что происходит при задержке от t 1до t 2 , и затем от t 2 до t 3 . Это в точности то же самое, что было с двумя последовательными приборами В и А. Тогда, следуя обозначениям, принятым в гл. 3, § 6, мы можем написать

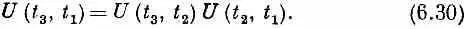
Иначе говоря, можно проанализировать любой интервал вре­мени, если мы умеем анализировать последовательность про­межуточных коротких интервалов. Мы просто перемножаем все куски; это и есть способ нерелятивистского анализа кван­товой механики.

Итак, задача состоит в том, чтобы узнать матрицу U ( t 2 , t 1) для бесконечно малого интервала времени — для t 2= t 1+D t . Спросим себя: если сейчас у нас есть состояние j, то как оно будет выглядеть через бесконечно малое время D t ? Посмотрим, как это можно расписать. Обозначим состояние в момент t через |y( t )> (мы указываем зависимость y от времени, чтобы было совершенно ясно, что речь идет об условиях в момент t ). Теперь зададим вопрос: каково будет положение вещей через короткое время D t ? Ответ таков:

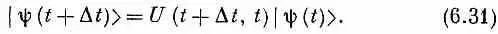
Здесь имеется в виду то же, что и в (6.25), а именно, что амплитуда обнаружить c в момент t + D t есть

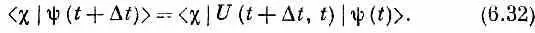
Поскольку мы еще не очень хорошо разбираемся в этих абстрактных вещах, то давайте спроецируем наши амплитуды в определенное представление. Умножая обе части (6.31) на < i |, получаем

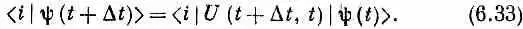
Можно также разложить и |y(t)> на базисные состояния и написать

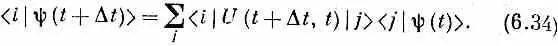
Понять это можно так. Если через C i ( t )= < i | y|( t )> обозна­чить амплитуду пребывания в базисном состоянии i в момент t , то можно считать эту амплитуду (помните, это просто число !) меняющейся во времени. Каждое С i становится функцией времени t . Кроме того, у нас есть информация о том, как амп­литуды С i меняются во времени. Каждая амплитуда в момент ( t + D t ) пропорциональна всем прочим амплитудам в момент t , умноженным на ряд коэффициентов. Обозначим U -матрицу через U ij , считая, что

U ij =< i | U | j > .

Тогда (6.34) можно записать так:

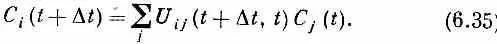
Вот как будет выглядеть динамика квантовой механики.

Нам пока мало известно об U ij . Мы знаем только, что при D t , стремящемся к нулю, ничего не должно произойти, просто должно получиться начальное состояние. Значит, U ij ®1 и U ij ®0 при i № j . Иными словами, U ij ® d ij при D t ®0. Кроме того, мы вполне вправе предположить, что при малых At каж­дый из U ij обязан отличаться от d ij на величину, пропорцио­нальную D t; так что можно писать

Однако обычно по историческим и по иным причинам из коэф­фициентов К ij выносят множитель

(- i/h) ; предпочитают писать

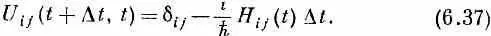
Это, разумеется, то же самое, что и (6.36). Если угодно, это просто определение коэффициентов H ij ( t ). Члены H ij — это как раз производные по t 2 от коэффициентов U ij ( t 2 , t 1) , вычисляемые при t 2 = t 1 = t ,