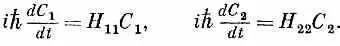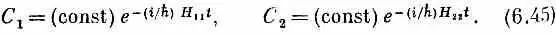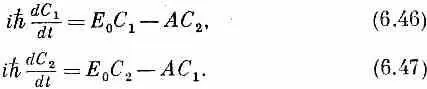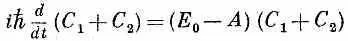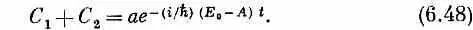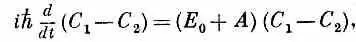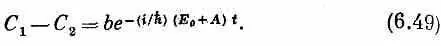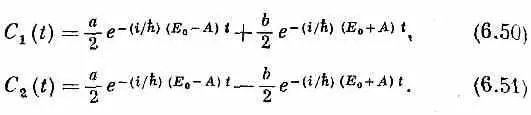Feynmann - Feynmann 8

Единственная трудность в том, что мы не знаем, что ставить вместо коэффициентов Н ij в (6.43). Но кое-что мы все же можем сказать. Предположим, что, если уж молекула оказалась в со­стоянии \1 >, тогда у нее не будет никакого шанса когда-либо по­пасть в состояние |2>, И наоборот. Тогда H 12и H 21будут оба равны нулю, и (6.43) примет вид

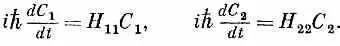
Эти уравнения легко решить; получается

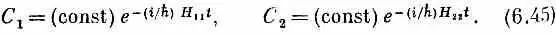
Это просто амплитуды стационарных состояний с энергиями E 1 = H 11 и E 2= H 22. Еще мы знаем, что у молекулы аммиака состояния | 1> и | 2> обладают определенной симметрией. Если природа ведет себя более или менее разумно, то матричные элементы Н 11 и H 22 должны равняться друг другу. Мы обозна­чим их через Е 0 , потому что они соответствуют энергии, ко­торой обладали бы состояния, будь H 12и H 21равны нулю.

Но (6.45) не отражает того, что на самом деле бывает с аммиаком. Оказывается, что аммиак имеет возможность про­толкнуть свой азот мимо трех водородов и перебросить его по ту сторону. Это очень трудно: чтобы азоту пройти полпути, нужна немалая энергия. Как же он может пройти на другую сторону, если он не располагает достаточной энергией? Просто имеется некоторая амплитуда того, что он проникнет сквозь энергетический барьер. В квантовой механике разрешается быстро проскакивать через энергетически нелегальную об­ласть. Стало быть, существует небольшая амплитуда того, что молекула, начав с состояния |1>, перейдет в состояние |2>. Коэффициенты Н 12 и Н 21 на самом деле не равны нулю. И опять из симметрии ясно, что они должны быть одинаковы, по край­ней мере по величине. И действительно, мы уже знаем, что вообще Н ij равняется комплексно сопряженной величине Н ji , т. е, они могут отличаться только фазой. Оказывается, как вы потом увидите, что без потери общности можно положить эти коэффициенты равными друг другу. Позднее нам будет удоб­нее считать их равными отрицательному числу; мы примем поэтому H 12= H 21=- А. Тогда получится следующая пара уравнений:

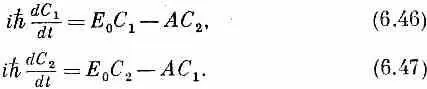
Эти уравнения достаточно просты и могут быть решены разным путем. Удобно решать их так. Складывая их, по­лучаем

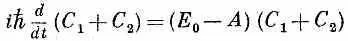
с решением

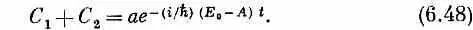
Вычитая затем (6.47) из (6.46), получаем

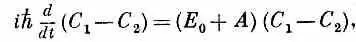
что дает

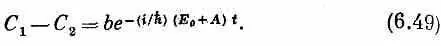
Две постоянные интегрирования мы обозначили а и b ; их надо выбрать так, чтобы получились подходящие начальные условия данной физической задачи. Наконец, складывая и вычитая (6.48) и (6.49), получаем C 1 и С 2:

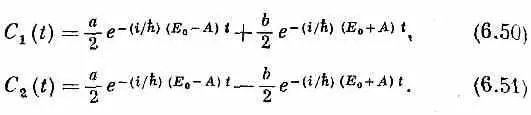
Они отличаются только знаком при втором слагаемом.

Решения-то мы получили, но что они значат? (В квантовой механике трудность не только в том, чтобы получить решения но и в том, чтобы разобраться в их смысле!) Заметьте, что при b = 0 оба решения обладают одинаковой частотой w =( E 0 - A )/ h Если все меняется с одной частотой, это значит, что система пребывает в состоянии с определенной энергией, в данном слу­чае с энергией (Е 0 - А). Значит, существует стационарное состояние с такой энергией; в нем обе амплитуды С 1 и C 2 равны друг другу. Мы приходим к выводу, что молекула аммиака обладает определенной энергией (Е 0 - А), если для атома азота одинакова амплитуда оказаться «вверху» и «внизу».

Имеется другое допустимое стационарное состояние, когда а=0; тогда обе амплитуды обладают частотой ( E 0 + A )/ h . Зна­чит, имеется другое состояние с определенной энергией (Е 0 + А), когда две амплитуды равны, но отличаются знаком: C 2 =- C 1 . Вот и все состояния с определенной энергией. В следующей главе мы поговорим о состояниях молекулы аммиака подроб­нее; здесь же мы отметим еще только некоторые особенности.