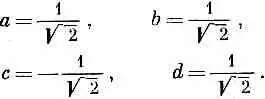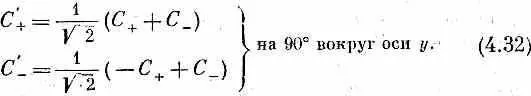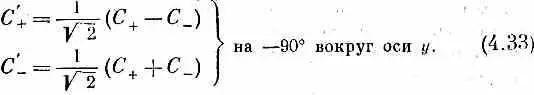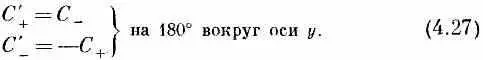
Продолжая размышлять о поворотах вокруг оси у, перейдем теперь к матрице преобразования для поворотов на 90°. Мы в состоянии установить ее вид, оттого что знаем, что два последовательных поворота на 90° вокруг одной и той же оси — это то же самое, что один поворот на 180°. Напишем преобразование для 90° в самой общей форме:
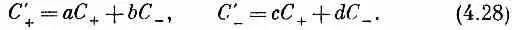
Второй поворот на 90° вокруг той же оси обладал бы теми же коэффициентами:
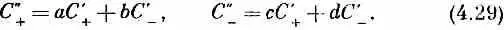
Подставляя (4.28) в (4.29), получаем
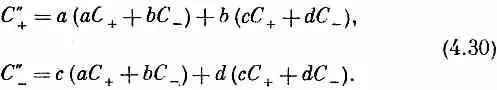
Однако из (4.27) нам известно, что

так что должно быть
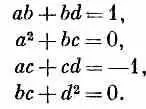 (4.31)
(4.31)
Этих четырех уравнений вполне хватает, чтобы определить все наши неизвестные а, b , с и d . Сделать это нетрудно. Посмотрите на второе и четвертое уравнения. Вы видите, что a 2= d 2, откуда либо a = d , либо a =- d . Но последнее отпадает, потому что тогда не выполнялось бы первое уравнение. Значит, d = a . А тогда сразу же выходит b =1/2 a и с=-1/2а. Теперь все выражено через а. Подставляя, скажем, во второе
уравнение значения b и с, получаем
а 2-1/4a 2= 0. или а 4= 1/ 4.
Из четырех решений этого уравнения только два приводят к детерминанту стандартной формы. Мы можем принять а=1/Ц2;
тогда
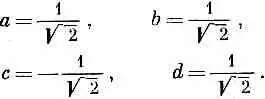
Иными словами, для двух приборов S и T при условии, что Т повернут относительно S на 90° вокруг оси у, преобразование имеет вид
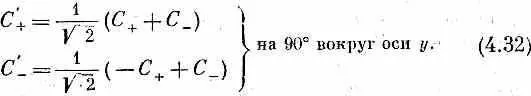
Эти уравнения можно, конечно, разрешить относительно С + и С - ; это даст нам преобразование при повороте вокруг оси у на -90°. Переставив еще и штрихи, мы напишем
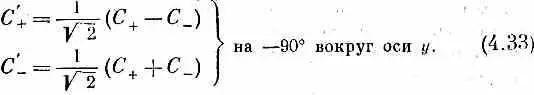
§ 5. Повороты вокруг оси х
Вы, пожалуй, подумаете: «Это становится смешным. Чему же нас теперь будут учить— поворотам на 47° вокруг оси у, потом на 33° вокруг x? Долго ли это будет продолжаться?» Нет, оказывается, я почти все рассказал. Зная только два преобразования — на 90° вокруг оси у и на произвольный угол вокруг оси z (как вы помните, именно с этого мы начали),— мы уже способны производить любые повороты.
Для иллюстрации предположим, что нас интересует поворот на угол а вокруг оси х. Мы знаем, как быть с поворотом на угол а вокруг оси z , но нам нужен поворот вокруг оси х. Как его определить? Сперва повернем ось z вниз до оси х, а это есть поворот на +90° вокруг оси у (фиг. 4.8).
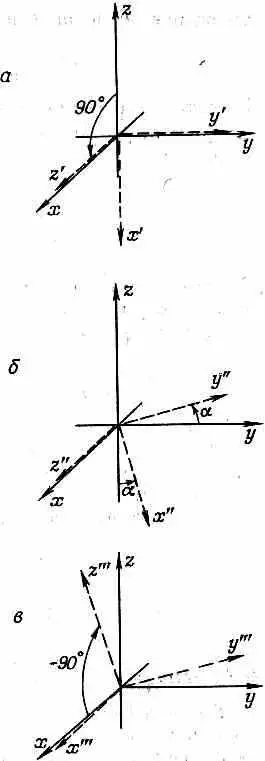
Фиг. 4.8. Поворот на угол a вокруг оси х равнозначен повороту на +90° вокруг оси у (а), за которым следует поворот ни а вокруг оси z ' (б), вслед за которым происходит поворот на -90° вокруг оси. у" (в).
Затем вокруг оси z ' повернемся на угол a. А потом повернемся на -90° вокpуг оси у".
Итог этих трех поворотов тот же самый, что при повороте вокруг оси х на угол a . Таково свойство пространства. (Все эти сочетания поворотов их результат очень трудно себе представить. Не правда ли, странно, что, живя в трех измерениях, мы все же с трудом воспринимаем, что произойдет, если сперва повернуться так, а потом еще как-нибудь. Вероятно, если бы мы были птицами или рыбами и если а мы на собственном опыте знали, что бывает, когда все время крутишь разные сальто в пространстве, нам было бы легче воспринимать подобные вещи.) Во всяком случае, давайте выведем преобразование для поворота на угол а вокруг оси х, пользуясь тем, что нам уже известно. При первом повороте на +90 ° вокруг оси у амплитуды следуют закону (4.32). Если повернутые оси обозначить х' , y' и z', то последующий поворот на угол а вокруг оси z переводит нас в систему отсчета х". у", z ", для которой
Читать дальше

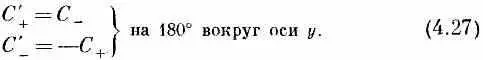
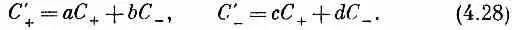
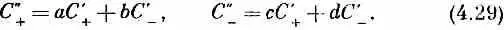
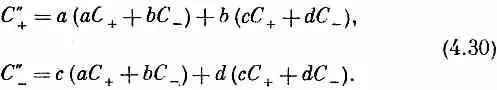

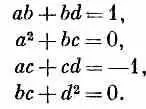 (4.31)
(4.31)