Ось у тоже без претензий. Частица в состоянии (+ z ) имеет равные шансы быть в состоянии ( + у) или (- у ) . Но теперь (согласно формуле для поворота на -90° вокруг оси х) амплитуды суть l/Ц2 и - i /Ц2. В этом случае разница в фазах двух амплитуд уже не 180°, как было для ( + х ) и (- х ) , а 90°. В этом-то и проявляется различие между х и у.
Вот еще пример. Пусть нам известно, что частица со спином 1/ 2находится в состоянии y, поляризованном вверх относительно оси А, определяемой углами q и j (фиг. 4.10).
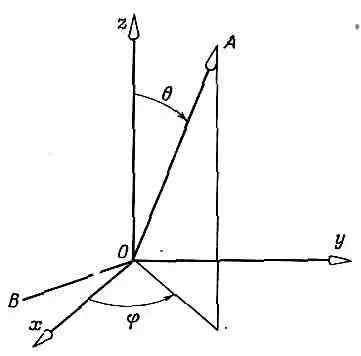
Фиг. 4.1 0 . Ось А, определяемая полярными углами q и j .
Мы хотим знать амплитуду +|y> того, что частица относительно оси z окажется в состоянии «вверх», и амплитуду -|y> того, что она окажется в состоянии «вниз» относительно той же оси z . Эти амплитуды мы можем найти, вообразив, что А есть ось z ' системы, у которой ось х' направлена произвольно, скажем лежит в плоскости, образованной А и z. Тогда можно перевести систему А в систему х, у, z тремя поворотами. Во-первых, надо сделать поворот на -p/2 вокруг оси A , что переведет ось x в линию В на рисунке. Затем повернуть на — 0 вокруг линии В (вокруг новой оси х системы А), чтобы ось А попала на ось z . И, наконец, повернуть вокруг оси z на угол (p/2-j).

Вспоминая, что вначале было только одно состояние (+) по отношению к А, получаем
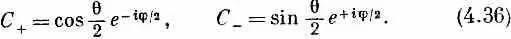
Мы хотели бы напоследок подытожить результаты этой главы в форме, которая окажется полезной для нашей дальнейшей работы. Во-первых, напомним, что наш основной результат (4.35) может быть записан в других обозначениях. Заметьте, что (4.35)— это то же самое, что и (4.4) Иначе говоря, в (4.35) коэффициенты при С +=<+S|y> и C' -= <- S |y> суть как раз амплитуды < jT | iS > в (4.4), амплитуды того, что частица в состоянии i по отношению к S окажется в состоянии j по отношению к Т (когда ориентация Т по отношению к S дается углами a, b и g) . Мы их также называли R TS ji в выражении (4.6). (Чего-чего, а обозначений у нас хватало!) Например, 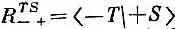 — это коэффициент при С + в формуле для С -, а именно i sin(a/2)exp[ i (b-g ) /2] . Поэтому сводку наших результатов мы можем дать в виде табл. 4.1.
— это коэффициент при С + в формуле для С -, а именно i sin(a/2)exp[ i (b-g ) /2] . Поэтому сводку наших результатов мы можем дать в виде табл. 4.1.
Было бы удобно иметь эти амплитуды расписанными для некоторых особо важных случаев. Пусть R z ( j ) — поворот на угол j вокруг оси z. Так же можно обозначить и соответствующую матрицу поворота (опуская молчаливо подразумеваемые индексы i и j ). В том же смысле R x ( j ) и R y ( j ) будут обозначать повороты на угол j вокруг оси х и оси у,
В табл. 4.2 мы приводим матрицы — таблицы амплитуд < jT | iS > , которые проецируют амплитуды из системы S в систему Т, где Т получается из S указанным поворотом.
* Нетрудно показать, что систему х, у, z можно перевести в систему х', у', z ' следующими тремя поворотами вокруг первоначальных осей: 1) повернуть на угол g вокруг первоначальной оси z ; 2) повернуть на угол а вокруг первоначальной оси х; 3) повернуть на угол b вокруг первоначальной оси z .
* Второе решение меняет все знаки у а , b , с, d и отвечает повороту на - 270°.
* Заметим, что если последовательность малых поворотов приведет в конце концов к первоначальной ориентации предмета, то всегда есть возможность, проследив всю историю, отличить поворот на 360° от поворота на 0° (но интересно, что для поворота на 720° это неверно).
Читать дальше



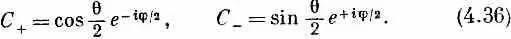
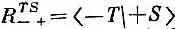 — это коэффициент при С + в формуле для С -, а именно i sin(a/2)exp[ i (b-g ) /2] . Поэтому сводку наших результатов мы можем дать в виде табл. 4.1.
— это коэффициент при С + в формуле для С -, а именно i sin(a/2)exp[ i (b-g ) /2] . Поэтому сводку наших результатов мы можем дать в виде табл. 4.1.










