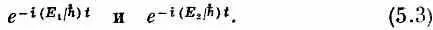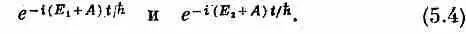Feynmann - Feynmann 8

Вот почему мы часто говорим, что атом на определенном энергетическом уровне находится в стационарном состоянии. Если вы что-то внутри него измеряете, вы обнаруживаете, что ничего (по вероятности) во времени не меняется. Чтобы вероят­ность менялась во времени, должна быть интерференция двух амплитуд при двух разных частотах, а это означало бы, что неизвестно, какова энергия. У предмета были бы одна ампли­туда пребывания в состоянии с одной энергией и другая ам­плитуда пребывания в состоянии с другой энергией. Так в квантовой механике описывается что-то, если поведение этого «чего-то» зависит от времени.

Если имеется случай, когда смешаны два различных со­стояния с разными энергиями, то амплитуды каждого из двух состояний меняются со временем согласно уравнению (5.2), скажем, как

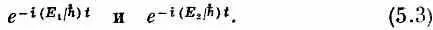
И если имеется комбинация этих двух состояний, то появится интерференция. Но заметьте, что добавление к обеим энергиям одной и той же константы ничего не меняет. Если кто-то другой пользовался другой шкалой энергий, на которой все энергии сдвинуты на константу (скажем, на А), то амплитуды оказаться в этих двух состояниях, с его точки зрения, были бы

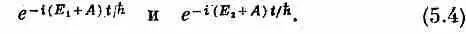
Все его амплитуды оказались бы умноженными на один и тот же множитель

ехр[- i ( A / h )/ t ] , и во все линейные комбинации, во все интерференции вошел бы тот же множитель. Вычисляя для определения вероятностей модули, он пришел бы к тем же ответам. Выбор начала отсчета на нашей шкале энергий ничего не меняет; энергию можно отсчитывать от любого нуля. В ре­лятивистских задачах приятнее измерять энергию так, чтобы в нее входила масса покоя, но для многих других нерелятивист­ских целей часто лучше вычесть из всех появляющихся энер­гий стандартную величину. Например, в случае атома обычно бывает удобно вычесть энергию М sс 2, где М s — масса отдель­ных его частей, ядра и электронов, отличающаяся, конечно, от массы самого атома. В других задачах полезно бывает вы­честь из всех энергий число M g c 2 , где M g — масса всего атома в основном состоянии; тогда остающаяся энергия есть просто энергия возбуждения атома. Значит, порой мы имеем право сдвигать, наш нуль энергии очень и очень сильно, и это все равно ничего не меняет (при условии, что все энергии в данном частном расчете сдвинуты на одно и то же число). На этом мы расстанемся с покоящимися частицами.

§ 2. Равномерное движение

Если мы предполагаем, что теория относительности верна, то частица, покоящаяся в одной инерциальной системе, в дру­гой инерциальной системе может оказаться в равномерном движении. В системе покоя частицы амплитуда вероятности для всех х, у и z одинакова, но зависит от t . Величина амплиту­ды для всех t одинакова, а фаза зависит от t . Мы можем по­лучить картину поведения амплитуды, если проведем линии равной фазы (скажем, нулевой) как функций х и t . Для части­цы в покое эти линии равной фазы параллельны оси х и рас­положены по оси t на равных расстояниях (показано пунктир­ными линиями на фиг. 5.1).

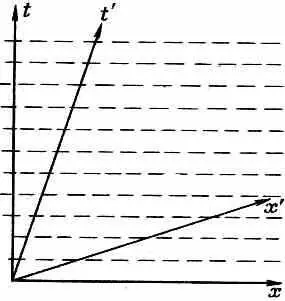
Фиг. 5.1. Релятивистское преоб­разование амплитуды покоящейся. частицы в систему х— t .

В другой системе, х' , у', z ' , t ' , движущейся относительно частицы, скажем, в направлении х, координаты х ' и t ' некото­рой частной точки пространства связаны с х и t преобразованием Лоренца. Это преобразование можно изобразить графи­чески, проведя оси х ' и t ' , как показано на фиг. 5.1 [см. гл. 17 (вып. 2), фиг. 17.2]. Вы видите, что в системе х '- — t ' точки рав­ной фазы вдоль оси t ' расположены на других расстояниях, так что частота временных изменений уже другая. Кроме того, фаза меняется и по х'. т. е. амплитуда вероятности должна быть функцией х'.

При преобразовании Лоренца для скорости v направлен­ной, скажем, вдоль отрицательного направления х. время t связано со временем t ' формулой